
Further Mathematics Questions and Answers
Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.

Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.
8
6
5
4
Correct answer is C
\((x * y) = \frac{x+y}{2}\)
\((3 * b) = \frac{3+b}{2}\)
\(x \circ y = \frac{x^{2}}{y}\)
\((\frac{3+b}{2}) \circ 48 = \frac{(\frac{3+b}{2})^{2}}{48} = \frac{1}{3}\)
\(\frac{(3+b)^{2}}{48 \times 4} = \frac{1}{3}\)
\((3 + b)^{2} = \frac{48 \times 4}{3} = 64\)
\(b^{2} + 6b + 9 = 64 \implies b^{2} + 6b + 9 - 64 = 0\)
\(b^{2} + 6b - 55 = 0 \implies b^{2} - 5b + 11b - 55 = 0\)
\(b(b - 5) + 11(b - 5) = 0 \implies (b - 5) = \text{0 or (} b + 11) = 0\)
Since b > 0, b - 5 = 0
b = 5.
Given that \(3x + 4y + 6 = 0\) and \(4x - by + 3 = 0\) are perpendicular, find the value of b.
4
3
\(\frac{1}{3}\)
\(\frac{1}{4}\)
Correct answer is B
When you have two lines, \(y_{1}, y_{2}\), perpendicular to each other, the product of their slopes = -1.
\(3x + 4y + 6 = 0 \implies 4y = -6 - 3x\)
\(\therefore y = \frac{-6}{4} - \frac{3}{4}x\)
\(\frac{\mathrm d y}{\mathrm d x} = \frac{-3}{4}\)
Also, \(4x - by + 3 = 0 \implies by = 4x + 3\)
\(y = \frac{4}{b}x + \frac{3}{b}\)
\(\frac{\mathrm d y}{\mathrm d x} = \frac{4}{b}\)
\(\frac{-3}{4} \times \frac{4}{b} = -1 \implies \frac{4}{b} = \frac{4}{3}\)
\(b = 3\)
Simplify: \((1 - \sin \theta)(1 + \sin \theta)\)
\(\sin^{2} \theta\)
\(\sec^{2} \theta\)
\(\tan^{2} \theta\)
\(\cos^{2} \theta\)
Correct answer is D
\((1 + \sin \theta)(1 - \sin \theta) = 1 - \sin \theta + \sin \theta - \sin^{2} \theta\)
\(= 1 - \sin^{2} \theta\)
Recall, \(\cos^{2} \theta + \sin^{2} \theta = 1\)
\(\therefore 1 - \sin^{2} \theta = \cos^{2} \theta\).
If \(\frac{1}{5^{-y}} = 25(5^{4-2y})\), find the value of y.
4
2
-4
-5
Correct answer is B
\(\frac{1}{5^{-y}} = 25(5^{4-2y})\)
\(\implies 5^{y} = (5^{2})(5^{4-2y})\)
\(5^{y} = 5^{2+4-2y}\)
Comparing bases, we have
\(y = 6 - 2y\)
\(3y = 6 \implies y = 2\)
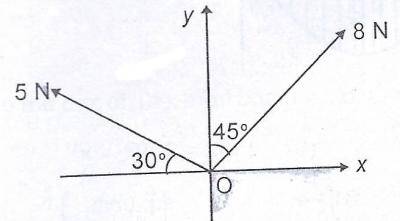
80.76°
75.00°
71.99°
15.00°
Correct answer is A
No explanation has been provided for this answer.