
Further Mathematics Questions and Answers
Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.

Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.
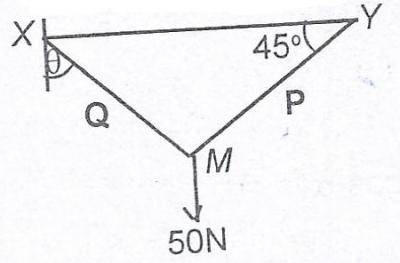
\frac{50 \cos \theta}{\sin (\theta + 45)°}
\frac{50 \cos \theta}{\cos (\theta + 45)°}
\frac{50 \sin \theta}{\cos (\theta + 45)°}
\frac{50 \sin \theta}{\sin (\theta + 45)°}
Correct answer is D
No explanation has been provided for this answer.
The distance between P(x, 7) and Q(6, 19) is 13 units. Find the values of x.
1 or -7
1 or 7
1 or 11
5 or -5
Correct answer is C
d = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}
13 = \sqrt{(x - 6)^{2} + (7 - 19)^{2}}
13^{2} = x^{2} - 12x + 36 + 144
169 = x^{2} - 12x + 180
x^{2} - 12x + 180 - 169 = 0 \implies x^{2} - 12x + 11 = 0
(x - 1)(x - 11) = 0 \implies x = \text{1 or 11}
If y = x^{2} - 6x + 11 is written in the form y = a(x - h)^{2} + k, find the value of (a + h + k).
-4
-3
0
6
Correct answer is D
y = x^{2} - 6x + 11
y = a(x - h)^{2} + k
a(x - h)^{2} + k = a(x^{2} - 2hx + h^{2}) + k
ax^{2} - 2ahx + ah^{2} + k = x^{2} - 6x + 11
Comparing, we have
a = 1
2ah = 6 \implies 2h = 6; h = 3
ah^{2} + k = 11 \implies (1 \times 3^{2}) + k = 11
9 + k = 11 \implies k = 2
\therefore a + h + k = 1 + 3 + 2 = 6
25
15
3\sqrt{7}
\sqrt{10}
Correct answer is A
Change in momentum = m (v - u)
= 5 \times (\begin{pmatrix} 4 \\ 7 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \end{pmatrix})
= 5 \times \begin{pmatrix} 3 \\ 4 \end{pmatrix}
= \begin{pmatrix} 15 \\ 20 \end{pmatrix}
|m(v - u)| = \sqrt{15^{2} + 20^{2}} = \sqrt{625} = 25
Find the value of the constant k for which a = 4 i - k j and b = 3 i + 8 j are perpendicular.
\frac{2}{3}
2
3
\frac{3}{2}
Correct answer is D
For perpendicular vectors, their dot product = 0.
(4i - kj). (3i + 8j) = 12 - 8k = 0
8k = 12 \implies k = \frac{3}{2}