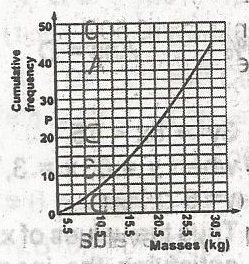
\(\frac{1}{2}(Q_3 - Q_1)\)
Q3 - Q2
Q3 - Q2
Q3 - Q1
Correct answer is D
No explanation has been provided for this answer.
\(\frac{1}{5}\)
\(\frac{2}{25}\)
\(\frac{4}{15}\)
\(\frac{3}{25}\)
Correct answer is D
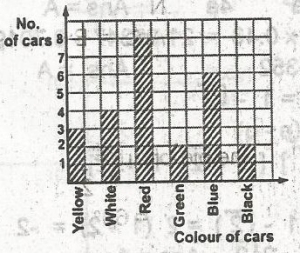
\(\begin{array}{c|c} \text{colour of cars} & \text{Number (frequency)} \\ \hline yellow & 3 \\white & 4\\ red & 8\\ green & 2\\ blue & 6\\ black & 2\\ \hline & 25 \\ \hline\end{array}\)
Thus, the fraction of the total numbers that are yellow is \(\frac{3}{25}\)
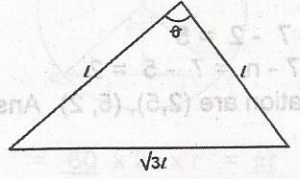
Find the value of \(\theta\) in the diagram
60o
100o
120o
30o
Correct answer is C
Using cosine formula (t\(\sqrt{3}\))2 = t2 + t2 - 2t2 cos\(\theta\)
3t2 = 2t2 - 2t2 cos\(\theta\) = 2t2(1 - cos\(\theta\))
1 - cos\(\theta\) = \(\frac{3t^2}{2t^2}\) = \(\frac{3}{2}\)
cos = 1 - \(\frac{3}{2} = -\frac{1}{2}\)
\(\theta\) = cos-1(-\(\frac{1}{2}\)) = 120o and 240o
N.B 0 \(\geq\) \(\theta\) 360
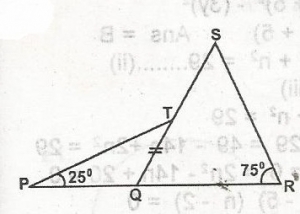
50o
25o
55o
45o
Correct answer is C
< T = \(\frac{x}{1}\) = 25o (PQ = QT)
< SQR = 2(25o) = 50o (sum of interior angle)
< Q + < R + < S = 180o
50o + 75o + < S = 180o = 125o + < S = 180o
< S = 180o - 125o = 55o
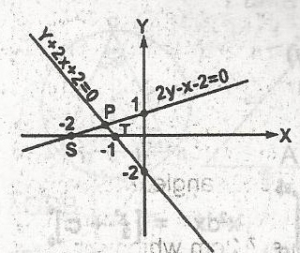
Triangle SPT is the solution of the linear inequalities
2y - x - 2 \(\leq\) 0, y + 2x + 2 \(\geq\) 0, x \(\geq\) 0
2y - x - 2 \(\geq\) 0, y + 2x + 2 \(\leq\) 0, -2 \(\geq\) x \(\geq\) -1
-2 \(\geq\) x \(\geq\) 2, y \(\leq\) 0, y + 2x + 2 \(\geq\) 0, x \(\geq\) 0
2y - x - 2 \(\geq\) 0, y + 2x + 2 \(\geq\) 0, y \(\leq\) 0, x \(\geq\) 0
Correct answer is C
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests