Solve \(1 + \sqrt[3]{ x - 3} = 4\)
30
6
12
66
Correct answer is A
\(1 + \sqrt [3]{x-3} = 4\)
= \(\sqrt[3]{x - 3} = 4 - 1\)
\(\sqrt[3]{x - 3} = 3 \)
take the cube of both sides
= x - 3 = 27
x = 27 + 3
∴ x = 30
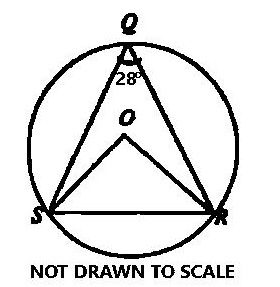
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
\(56^0\)
\(28^0\)
\(76^0\)
\(62^0\)
Correct answer is D
∠SOR = 2 × 28° = 56° (angle at the centre is twice the angle at the circumference)
From ∆SOR
|OS| = |OR| (radii)
So, ∆SOR is isosceles.
∠ORS = \(\frac{180^0 - 56^0}{2} = \frac{124^0}{2}\) ( base angles of isosceles triangle are equal)
∴ ∠ORS = 62°
6 days
8 days
10 days
12 days
Correct answer is A
12 men working 8 hours a day can complete the work in 4 days
12 men working 1 hour a day will complete the same work in (8 x 4) days [working less hours a day means they have to work for more days]
1 man working 1 hour a day will complete same work in (8 x 4 x 12) days [fewer number of men working means the remaining ones will have to work for more days ]
So, it will take 1 man working 1 hour a day to complete a piece of work in (8 x 4 x 12) days = 384 days
Now,
1 man working 16 hours a day will complete the piece of work in (384/16) days = 24 days [working more hours a day means less days to complete the work]
∴ 4 men working 16 hours a day will complete the piece of work in (24/4) days = 6 days [more men working means fewer days to complete the work]
ALTERNATIVELY
12 x 8 x 4 = 4 x 16 x d
⇒ d = \(\frac{12 \times 8 \times 4}{4 \times 16}\)
⇒ d = \(\frac{384}{64}\)
⇒ d = 6
∴ 4 men working 16 hours a day will complete the piece of work in 6 days
VIP = 80, Regular = 100
VIP = 60, Regular = 120
VIP = 60, Regular = 100
VIP = 80, Regular = 120
Correct answer is D
Let \(x\) = number of VIP tickets sold and
\(y\) = number of regular tickets sold
Total number of tickets sold = 200
⇒ \(x\) + \(y\) = 200 ---- (i)
If it costs ₦1,200 for a VIP ticket, then it costs ₦1200x for \(x\) number of VIP tickets sold and
If it costs ₦700 for a regular ticket, then it costs ₦700\(y\) for \(y\) number of VIP tickets sold
The total amount realised from the sale of tickets = ₦180,000
⇒ 1200\(x\) + 700\(y\) = 180000 ----- (ii)
From equation (i)
\(x\) = 200 - \(y\) ----- (iii)
Substitute (200 - \(y\)) for \(x\) in equation (ii)
⇒ 1200(200 - \(y\)) + 700\(y\) = 180000
⇒ 240000 - 1200\(y\) + 700\(y\) = 180000
⇒ 240000 - 500\(y\) = 180000
Collect like terms
⇒ 240000 - 180000 = 500\(y\)
⇒ 60000 = 500\(y\)
⇒ \(y = \frac{60000}{500} = 120\)
Substitute 120 for \(y\) in equation (iii)
⇒ \(x = 200 - 120\)
⇒ \(x = 80\)
∴ The total number of VIP tickets sold is 80 and regular is 120
7 significant figures
3 significant figures
4 significant figures
5 significant figures
Correct answer is D
The two trailing zeros in the number are not significant, but the other five are, making it a five-figure number.
JAMB Subjects
Aptitude Tests