Find the value of \(\theta\) in the diagram
...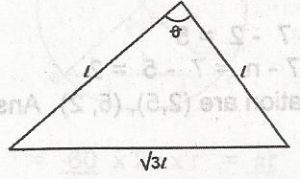
Find the value of \(\theta\) in the diagram
60o
100o
120o
30o
Correct answer is C
Using cosine formula (t\(\sqrt{3}\))2 = t2 + t2 - 2t2 cos\(\theta\)
3t2 = 2t2 - 2t2 cos\(\theta\) = 2t2(1 - cos\(\theta\))
1 - cos\(\theta\) = \(\frac{3t^2}{2t^2}\) = \(\frac{3}{2}\)
cos = 1 - \(\frac{3}{2} = -\frac{1}{2}\)
\(\theta\) = cos-1(-\(\frac{1}{2}\)) = 120o and 240o
N.B 0 \(\geq\) \(\theta\) 360
Similar Questions
In the diagram PQ and MN are straight lines. Find the value of x ...
Evaluate \(\frac{5}{8} - \frac{3}{4} ÷ \frac{5}{12} \times \frac{1}{4}\)...
In the diagram, MN//PO, < PMN = 112o, < PNO = 129o...
Rationalize \(\frac{5\sqrt{7} - 7\sqrt{5}}{\sqrt{7} - \sqrt{5}}\) ...
\((\sqrt[4]{3} + \sqrt[4]{2})(\sqrt[4]{3} - \sqrt[4]{2})(\sqrt{3} + \sqrt{2})\) is equal to...