
Further Mathematics Questions and Answers
Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.

Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.
\(\frac{\sqrt{3} \tan x - 1}{\sqrt{3} + \tan x}\)
\(\frac{\sqrt{3} \tan x}{\sqrt{3} + \tan x}\)
\(\frac{\sqrt{3} \tan x + 1}{\sqrt{3} - \tan x}\)
\(\frac{3 \tan x - 1}{\sqrt{3} - \tan x}\)
Correct answer is A
No explanation has been provided for this answer.
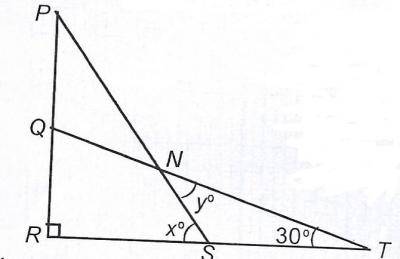
\(y = \frac{1}{2}x + 30\)
\(y = \frac{1}{2}x + 30\)
\(y = x + 30\)
\(y = x - 30\)
Correct answer is D
No explanation has been provided for this answer.
11.6 N
11.7 N
11.8 N
11.9 N
Correct answer is B
\(F = F \cos \theta i + F \sin \theta j\) (Resolving F into its components)
\(F_{1} = (10 N, 090°) = 10 \cos 90 i + 10 \sin 90 j\)
= \(10 j\)
\(F_{2} = (6 N, 180°) = 6 \cos 180 i + 6 \sin 180 j\)
= \(-6 i\)
\(R = - 6 i + 10 j\)
\(|R| = \sqrt{(-6)^{2} + (10)^{2}}\)
= \(\sqrt{136}\)
= 11.7 N
3.2 years
2.6 years
1.9 years
1.8 years
Correct answer is D
| \(x\) | 5 | 6 | 6 | 8 | 10 | Total |
| \(x - \bar{x}\) | -2 | -1 | -1 | 1 | 3 | |
| \((x - \bar{x})^{2}\) | 4 | 1 | 1 | 1 | 9 | 16 |
Mean (\(\bar{x}\)) = \(\frac{5 + 6 + 6 + 8 + 10}{5} \)
= \(\frac{35}{5} = 7\)
\(SD = \sqrt{\frac{\sum (x - \bar{x})^{2}}{n}}\)
= \(\sqrt{\frac{16}{5}} \)
= \(\sqrt{3.2}\)
\(\approxeq 1.8 years\)
\(\frac{3}{7}\)
\(\frac{21}{50}\)
\(\frac{7}{15}\)
\(\frac{49}{100}\)
Correct answer is C
\(P(\text{both bulbs are good}) = \frac{7}{10} \times \frac{6}{9}\)
= \(\frac{7}{15}\)