1,121.
Calculate the standard deviation of the following marks; 2, 3, 6, 2, 5, 0, 4, 2
A.
1.5
B.
1.7
C.
1.8
D.
1.9
Correct answer is C
| x | 2 | 3 | 6 | 2 | 5 | 0 | 4 | 2 | 24 |
| x - \(\bar{x}\) | -1 | 0 | 3 | -1 | 2 | -3 | 1 | -1 | |
| \((x - \bar{x})^2\) | 1 | 0 | 9 | 1 | 4 | 9 | 1 | 1 | 26 |
Mean = \(\frac{24}{8} = 3\)
Standard deviation = \(\sqrt{\frac{26}{8}}\)
= \(\sqrt{3.25}\)
= 1.802 \(\approeq\) 1.8
1,122.
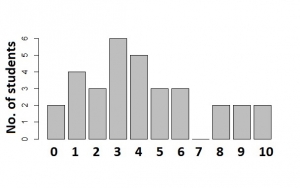

A.
38
B.
32
C.
15
D.
11
Correct answer is D
2 + 3 + 4 + 5 + 6 + 3 +3 + 0 + 2 + 2 + 2 = 32
1,123.
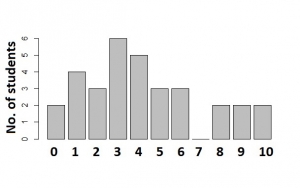

A.
15
B.
11
C.
10
D.
17
Correct answer is D
Students that scored 4 and above = 5 + 3 + 3 + 0 + 2 + 2 + 2
= 17
1,124.
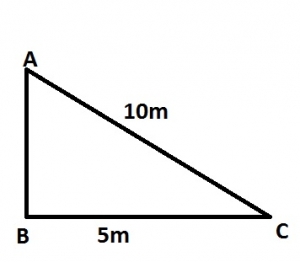
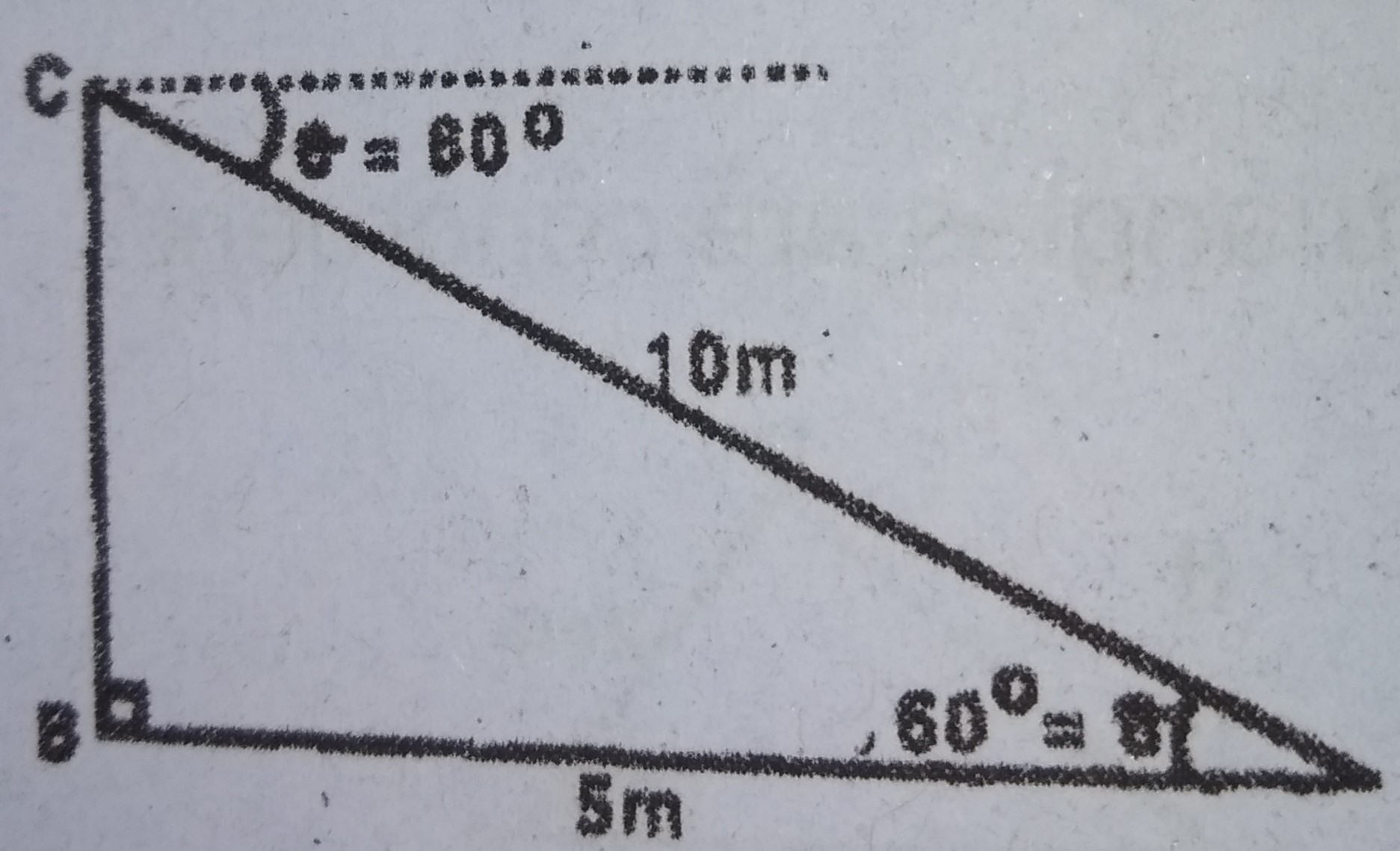

A.
63o
B.
60o
C.
45o
D.
27o
Correct answer is B

In triangle ABC, \(\frac{BC}{AC} = \cos \theta\)
\(\implies \cos \theta = \frac{5}{10} = 0.5\)
\(\theta = \cos^{-1} (0.5) = 60°\)
1,125.
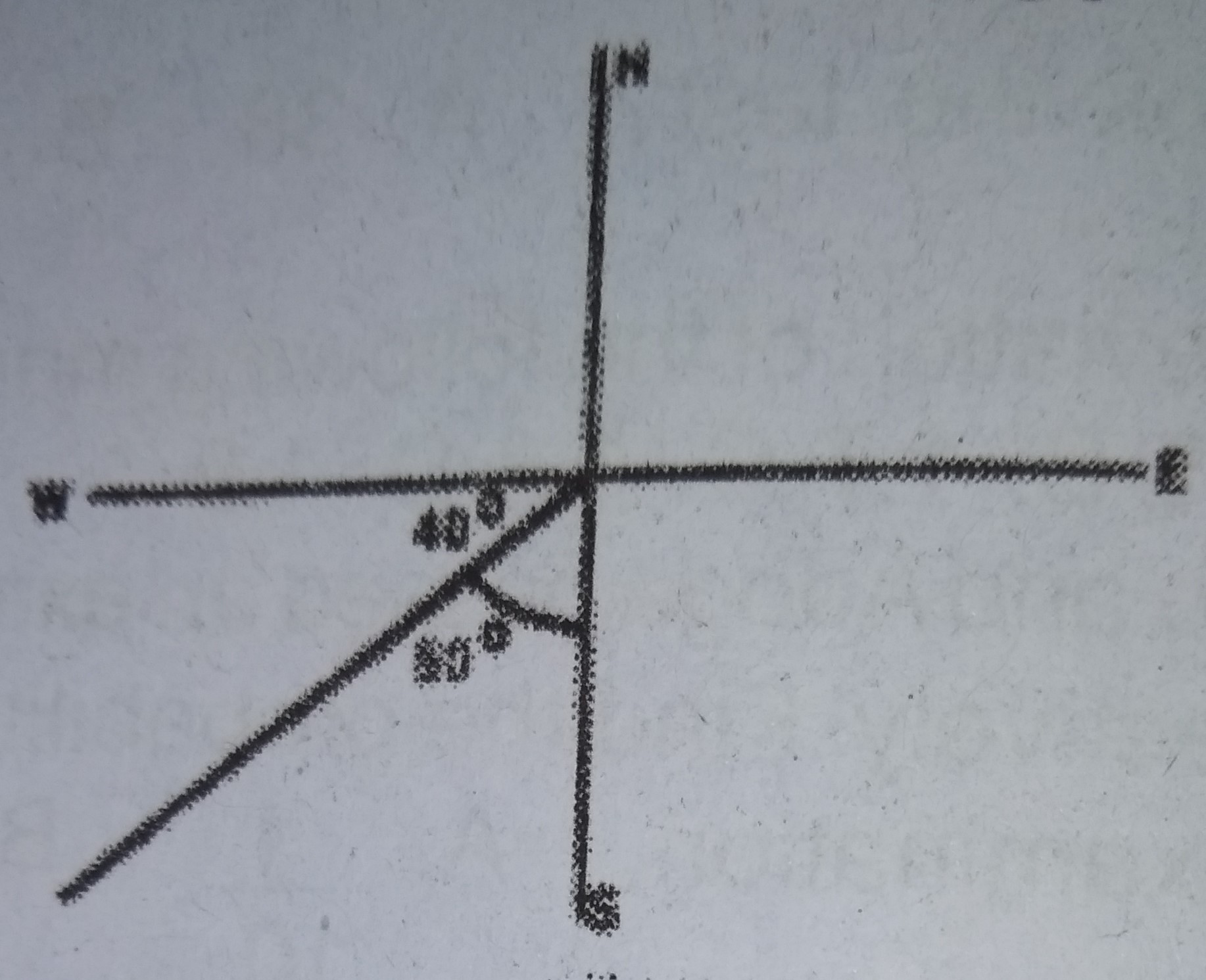
Which of the following bearings is equivalent to S50°W?
A.
040o
B.
130o
C.
220o
D.
230o
Correct answer is D

p>S50°W = 180° + 50°
= 230°
WAEC Subjects
Aptitude Tests