WAEC Mathematics Past Questions & Answers

x̄ = \(\frac{ 14 + 15 + 16 +17 + 18 + 19}{6} = \frac{99}{6}\) = 16.5

M . D = \(\frac{ (14 - 16.5) + (15 - 16.5) + (16 - 16.5) + (17 - 16.5) + (18 - 16. 5) + (19 - 16.5) }{ 6}\)

M.D = \(\frac{(-2.5) + (-1.5) + (-0.5) + (0.5) + (1.5) + (2.5)}{6}\)

Taking the absolute value of the deviations

M.D = \(\frac{2.5 + 1.5 + 0.5 + 0.5 + 1.5 + 2.5}{6}\)

M.D = \(\frac{9}{6}\) = 1.5

\(M ∝ n^2\sqrt{q}\)

\(M = Kn^2\sqrt{q}\)

K = \(\frac{M}{n^2\sqrt{q}}\)

K = \(\frac{24}{2^2\sqrt4}\)

k = \(\frac{24}{8} = 3\)

Now, let's find M when  n = 5 and q = 9

M = \(Kn^2\sqrt{q}\)

M = \( 3\times5^2\sqrt9\)

\(M = 3\times25\times3\)

Therefore, M = 225.

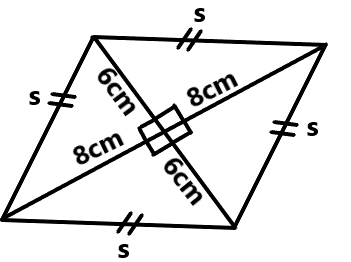
In a rhombus, the diagonals are perpendicular bisectors of each other, and they bisect the angles of the rhombus. This means that a rhombus is essentially made up of four congruent right-angled triangles.
We can use the Pythagorean theorem to find the length of one side of the rhombus (s)
\(s^2 = 8^2 + 6^2\)
\(s^2 = 64 + 36\)
\(s^2 = 100\)
s = \(\sqrt{100}\) 
s =10 cm
So, the length of each side of the rhombus is 10 cm.

2x - 3y = -11 --- (i)
3x + 2y = 3 --- (ii)
Multiply equation (i) by 3 and equation (ii) by 2
6x - 9y = -33 --- (iii)
6x + 4y = 6 --- (iv)
Subtract equation (iii) from (iv)
13y = 39

y = \(\frac{39}{13}\) = 3 

substitute (3) for y in equation (ii)
3x + 2(3) = 3
3x + 6 = 3
3x = 3 - 6
3x = -3
x  = \(\frac{-3}{3}\) = - 1

Now,
\((y - x)^2 = (3 - (-1))^2\)
= \((3 + 1)^2\)
= \(4^2\)
= 16

Error = 16.8 - 15 = 1.8cm

% error = \(\frac{error}{ Actual value}\times 100%\)

=      \(\frac{1.8}{ 15}\times100%\)

=  \(0.12\times100%\)

   =   12.00%