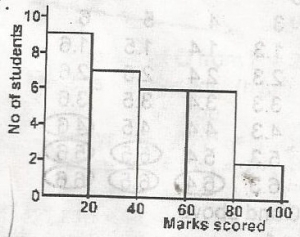
14%
40%
46\(\frac{3}{4}\)%
53\(\frac{1}{3}\)%
Correct answer is C
This histogram is transferred into this frequency table
\(\begin{array}{c|c} Marks & 20 & 40 & 60 & 80 & 100 \\ \hline students & 9 & 7 & 6 & 6 & 2\end{array}\)
Students who scored more than 40 = 6 + 6 + 2 = 14
i.e. \(\frac{14}{30}\) x 100% = 46\(\frac{3}{4}\)%
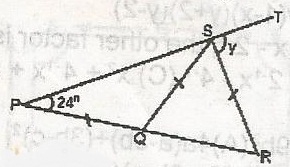
If PST is a straight line and PQ = QS = SR in the diagram, find y.
24o
48o
72o
84o
Correct answer is A
< PSQ = < SQR = < SRQ = 24o
< QSR = 180o - 48o = 132o
< PSQ + < QSR + y + 180 (angle on a straight lines)
24 + 132 + y = 180o = 156o + y = 180
y = 180o - 156o
= 24o
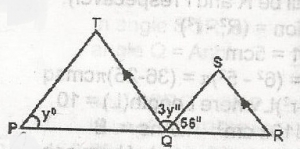
If PQR is a straight line with QS = QR, calculate TPQ, If QT\\SR and TQS = 3yo
62o
56\(\frac{3}{2}\)o
20\(\frac{3}{2}\)o
18o
Correct answer is C
Since QS = QR
then, angle SQR = angle SRQ
2 SQR = 180 - 56, SQR = \(\frac{124}{2}\) = 62o
QTP = 62o
QTP = 62o, corresponding angle
3y + 56 + 62 = 180 = 3y = 180 - 118
3y = 62 = 180
3y = 180 - 118
3y = 62
y = \(\frac{62}{3}\)
= 20\(\frac{3}{2}\)
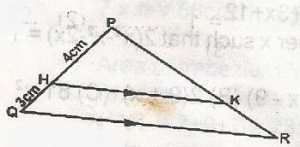
In the diagram, HK is parallel to QR, PH = 4cm and HQ = 3cm. What is the ratio of KR:PR?
7:3
3:7
3:4
4:3
Correct answer is B
In \(\bigtriangleup\)PHK and \(\bigtriangleup\)PAR = \(\frac{PH}{PQ} = \frac{PK}{PR}\)
\(\frac{4}{7} \times \frac{PR-KR}{PR}\)
4PR = 7(PR - KR) = 7PR - 7KR
\(\frac{KR}{PR} = \frac{3}{7}\)
KR:PR = 3:7
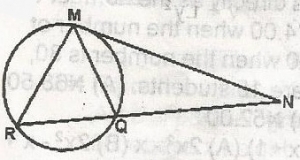
120o
110o
60o
20o
Correct answer is D
QMN = 60o
MRQ = 60o(angle in the alternate segment are equal)
MQN = 80o(angle sum of a \(\bigtriangleup\) = 180o)
60 = x = 80o(exterior angle = sum of opposite interior angles)
x = 80o - 60o = 20o
RMQ = 20o
JAMB Subjects
Aptitude Tests