(x − 5) 2
(x + 5)(x + 4)
(x – 5)(x + 3)
(x + 3) 2
Correct answer is B
\( x^2 + 9x + 20 \)
Find the two numbers whose product is 20 and its sum is 9}
\( 5x \times 4x = 20x^2\)
\(5x + 4x = 9x\)
\((x^2 + 5x) + (4x + 20)\)
\(
x(x + 5)+ 4(x + 5)
= (x + 5)(x + 4)\)
1 \( \frac{3}{8}\)
2 \( \frac{3}{4}\)
4 \( \frac{3}{8}\)
3 \( \frac{1}{5}\)
Correct answer is C
1¼ ÷ [ 2 ÷ ¼] of 28
Apply BODMAS rules
\( \frac{5}{4}\) ÷ [ 2 ÷ ¼ × 28 ]
\( \frac{5}{4} ÷ \frac{2}{7} \)
\( \frac{5}{4} × \frac{7}{2} \)
\( \frac{35}{8}\)
= \(4 \frac{3}{8}\)
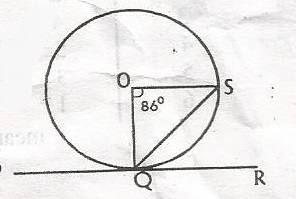
43o
47o
54o
86o
Correct answer is A
Construction: draw a line from Q to point P and another line from S to point P.
< SOQ = 2< QPS (< at centre is twice < on the circumference)
< QPS \(\frac{86}{2} = 43\)
< SQR = < QPS ( < between a chord and tangent = < in the alternate segment)
< SQR = 43o
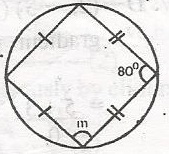
Determine the value of m in the diagram
80o
90o
110o
150o
Correct answer is B
No explanation has been provided for this answer.
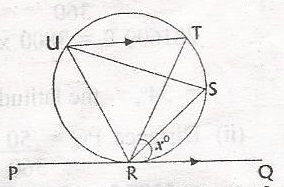
2xo
(90 - x)o
(90 + x)o
(180 - 2x)o
Correct answer is D
< URT = < TRQ (angle alternate a tangent and a chord equal to angle in the alternate segment)
< RUT = xo
In \(\bigtriangleup\) URT
< RUT + < RUT + < UTR = 180o (sum of int. < s of \(\bigtriangleup\))
< URT + x + x = 180o
< URT = 180o - 2x
WAEC Subjects
Aptitude Tests