In the figures, PQ is a tangent to the circle at R and UT is...
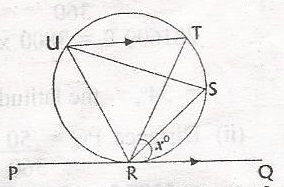
In the figures, PQ is a tangent to the circle at R and UT is parallel to PQ. if < TRQ = xo, find < URT in terms of x
A.
2xo
B.
(90 - x)o
C.
(90 + x)o
D.
(180 - 2x)o
Correct answer is D
< URT = < TRQ (angle alternate a tangent and a chord equal to angle in the alternate segment)
< RUT = xo
In △ URT
< RUT + < RUT + < UTR = 180o (sum of int. < s of △)
< URT + x + x = 180o
< URT = 180o - 2x
Similar Questions
Simplify (34 of 49 ÷ 912) ÷ 1519...
If y varies directly s the square root of (x + 1) and y = 6 when x = 3, find x when y = 9 ...
In the diagram above, |XR| = |RY| = |YZ| and ∠XRY = ∠YRZ = 62o, Calculate ∠XYZ ...
Find the mean of the following 24.57, 25.63, 24.32, 26.01, 25.77...
The derivatives of (2x + 1)(3x + 1) is ...