40 cm\(^2\)
48 cm\(^2\)
80 cm\(^2\)
120 cm\(^2\)
Correct answer is C
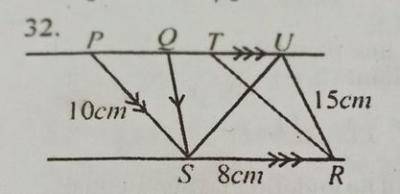
Area PTRS = 10cm x 8cm
= 80cm
55\(^o\)
36\(^o\)
25\(^o\)
22\(^o\)
Correct answer is C
L = \(\frac{\theta}{360^o}\) = 2\(\pi\)
\(\frac{55}{36} = \frac{\theta}{360^o} \times 2 \times \frac{22}{7} \times 3.5\)
\(\theta = \frac{360 \times 55 \times 44 \times 0.5}{3 \times 44 \times 0.5}\)
= \(\theta = 25^o\)
200\(^o\)
100\(^o\)
120\(^o\)
90\(^o\)
Correct answer is B
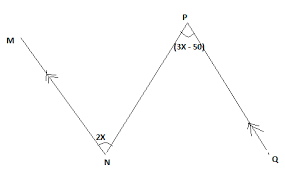
2x = 3x - 50 alternate angle
50\(^o\) = 3x - 2x
50\(^o\) = x
< NPQ = (3x - 50)\(^o\)
= 3(500)\(^o\) - 50
= 150 - 50 = 100\(^o\)
Each interior angle of a regular polygon is 168\(^o\). Find the number of sides of the polygon
30
36
24
18
Correct answer is A
Exterior angle = 180\(^o\) - 168\(^o\)
Number of sides = \(\frac{360^o}{12}\)
= 30\(^o\)
10cm
6cm
8cm
7cm
Correct answer is D
Volume = \(\frac{1}{3}\) x 9 x 5 x h
105 = \(\frac{1}{3}\) x 9 x 5 x h
\(\frac{105}{15} = \frac{15h}{15}\)
h = 7cm
WAEC Subjects
Aptitude Tests