1,431.
Find the median of the set of numbers 12, 15, 13, 14, 12, 12.
A.
12
B.
12.5
C.
13
D.
13.5
E.
14
Correct answer is B
12, 12, 12, 13, 14, 15
Median = \(\frac{12 + 13}{2}\)
= 12.5
1,432.

A.
4.2
B.
4.5
C.
4.8
D.
5.0
E.
5.2
Correct answer is C
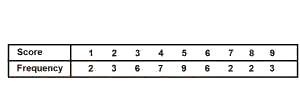
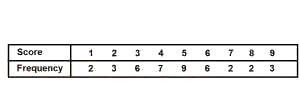
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total |
| f | 2 | 3 | 6 | 7 | 9 | 6 | 2 | 2 | 3 | 40 |
| fx | 2 | 6 | 18 | 28 | 45 | 36 | 14 | 16 | 27 | 192 |
Mean = \(\frac{\sum fx}{\sum f}\)
= \(\frac{192}{40}\)
= 4.8
1,433.

A.
(5,5)
B.
(5,6)
C.
(6,5)
D.
(9,4)
E.
(9,5)
Correct answer is A
Mode = 5
Median = 5
(m, n) = (5, 5)
1,434.
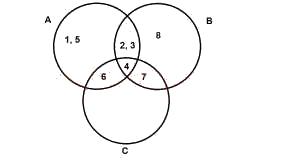

What is A∩B in the diagram above?
A.
(2,3)
B.
(2,3,4)
C.
(1,2,3)
D.
(2,3,8)
E.
(6,4,7)
Correct answer is B
No explanation has been provided for this answer.
1,435.
Find the median of the following set of numbers: 28, 29, 39, 38, 33, 37, 26, 20, 15, 25
A.
33
B.
29.5
C.
29
D.
28.5
E.
28
Correct answer is D
15, 20, 25, 26, 28, 29, 33, 37, 38, 39
median = \(\frac{28 + 29}{2}\)
= 28.5
WAEC Subjects
Aptitude Tests