31/2cm
7cm
1O1/2cm
14cm
21cm
Correct answer is B
The length of the arc subtended by the sector of angle 120° = circumference of the base of the cone.
\(\frac{120}{360} \times 2 \times \frac{22}{7} \times 21 = 2\pi r\)
\(44 = 2\pi r\)
\(r = 22 \div \pi\)
\(r = 22 \times \frac{7}{22}\)
r = 7 cm
104o
100o
80o
50o
24o
Correct answer is D
Latitudinal difference = 65° - 15°
= 50°
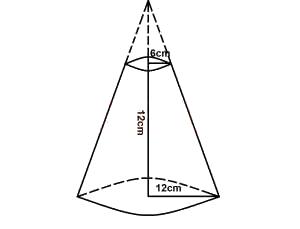
12cm
15cm
18cm
24cm
30cm
Correct answer is D
Considering the smaller and larger triangle, these two are similar triangles. Hence,
If the height of the smaller triangle = h,
\(\therefore \frac{h}{6} = \frac{h + 12}{12}\)
\(12h = 6h + 72 \implies 6h = 72\)
\(h = 12 cm\)
\(\therefore\) The height of the cone = 12 + 12 = 24 cm
3cm
6cm
9cm
12cm
More information is needed
Correct answer is B
\(Volume = \frac{4}{3} \pi r^3 = k\) ...(i)
\(S.A = 4\pi r^2 = k\) ... (ii)
Divide (i) by (ii),
\(\frac{4}{3} \pi r^3 \div 4\pi r^2 = \frac{k}{k}\)
\(\frac{r}{3} = 1 \implies r = 3cm\)
Diameter = 2 x 3cm = 6cm
37 5/7cm2
66cm2
75 3/7cm2
78 2/7cm2
88cm2
Correct answer is B
T.S.A of a cone = \(\pi r^2 + \pi rl\)
= \(\frac{22}{7} \times 3^2 + \frac{22}{7} \times 3 \times 4\)
= \(\frac{198}{7} + \frac{264}{7}\)
= \(\frac{462}{7}\)
= 66 cm\(^2\)
WAEC Subjects
Aptitude Tests