Express as a single fraction: \(\frac{x}{x-2}-\frac{x+2}{x+3}\)
\(\frac{2x^2 - 3x - 4}{(x-2)(x+3)}\)
\(\frac{2x^2 + 3x - 4}{(x-2)(x+3)}\)
\(\frac{2}{(x-2)(x+3)}\)
\(\frac{ 3x + 4}{(x-2)(x+3)}\)
\(\frac{3x - 4}{(x-2)(x+3)}\)
Correct answer is D
\(\frac{x}{x-2}-\frac{x+2}{x+3}\)
\(\frac{[x][x+3] - [x+2][x-2]}{[x-2][x+3]}\)
= \(\frac{x^2 + 3x - x^2 - 4}{[x-2][x+3]}\)
= \(\frac{3x - 4}{[x-2][x+3]}\)
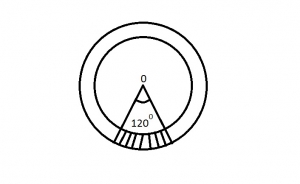
\(\frac{1}{3}\pi cm^2\)
\(\pi cm^2\)
\(3\pi cm^2\)
\(23\pi cm^2\)
\(46\pi cm^2\)
Correct answer is D
\(\frac{120\pi}{360}(R^2 - r^2)\\
\frac{1}{3}\times \pi (13^2 - 10^2)\\
\frac{1}{3}\times \pi \times 69 = 23\pi cm^2\)
The radius of a geographical globe is 60cm. Find the length of the parallel of latitude 60oN
\(66\pi cm\)
\(60\pi cm\)
\(30\pi cm\)
\(15\pi cm\)
\(6\pi cm\)
Correct answer is B
No explanation has been provided for this answer.
Given that \(\frac{6x-y}{x+2y}=2\), find the value of \(\frac{x}{y}\)
\(\frac{3}{8}\)
\(\frac{5}{8}\)
\(\frac{4}{5}\)
\(\frac{5}{4}\)
\(\frac{8}{5}\)
Correct answer is D
\(\frac{6x-y}{x+2y}=2\)
→ \((6x-y) = (x+2y)2\)
= 6x - y = 2x + 4y
Collect like terms: 6x - 2x = 4y + y
→ 4x = 5y
\(\frac{x}{y} = \frac{4}{5}\)
If h(m+n) = m(h+r) find h in terms of m, n and r
\(h=\frac{mr}{2m+n}\)
\(h=\frac{mr}{n+m}\)
\(h=\frac{m+n}{n}\)
\(h=\frac{m+n}{m}\)
\(h=\frac{mr}{n}\)
Correct answer is E
\(h(m+n) = m(h+r)\\
hm+hn=hm+mr\\
hn=mr\\
h=\frac{mr}{n}\)
WAEC Subjects
Aptitude Tests