Given that \(p = x-\frac{1}{x} and\hspace{1mm}q = x^2 + \frac{1}{x^2}\) express q in terms of p.
(p2 + 2)
(p - 2) 2
(p + 2) 2
(p2 - 2)
Correct answer is A
Given \(p = x - \frac{1}{x}\); \(q = x^2 + \frac{1}{x^2}\).
\(p^2 = (x - \frac{1}{x})(x - \frac{1}{x})\)
\(p^2 = x^2 + \frac{1}{x^2} - 2\)
\(p^2 = q - 2 \implies q = p^2 + 2\)
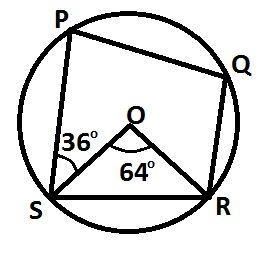
In the diagram O is the center of the circle, ∠SOR = 64° and ∠PSO = 36°. Calculate ∠PQR
100o
96o
94o
86o
Correct answer is D
< OSR = < ORS = \(\frac{180° - 64°}{2}\) = 58°
< PSR = 36° + 58° = 94°
< PSR + < PQR = 180°
94° + < PQR = 180° \(\implies\) < PQR = 180° - 94° = 86°
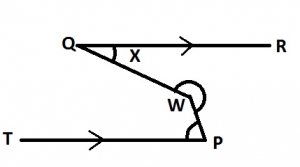
In the diagram, \(QR||TP and W\hat{P}T = 88^{\circ} \). Find the value of x
92o
68o
67o
23o
Correct answer is C
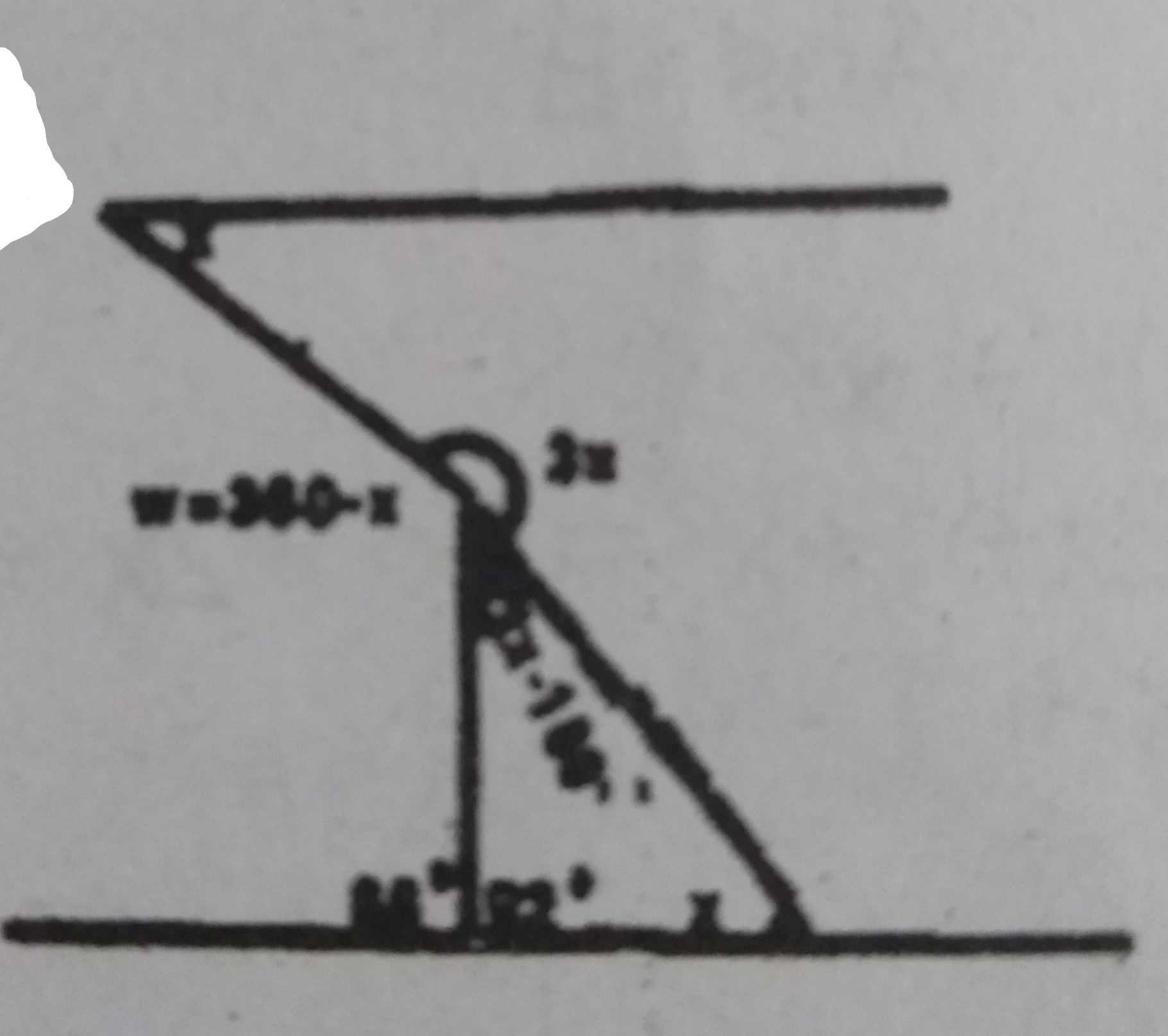
Sum of the angles in a triangle = 180°
3x - 180° + 92° + x = 180°
4x - 88° = 180°
4x = 268°
x = 67°
60km/hr
80km/hr
90km/hr
108km/hr
Correct answer is C
\(speed = \frac{distance}{time}\\
72 = \frac{60}{time}\\
t = \frac{60}{72} = \frac{5}{6}hr\)
time lost = 10mis \(= \frac{10}{60}hr = \frac{1}{6}\)
Time required for the journey
\(=\frac{5}{6}-\frac{1}{6} = \frac{2}{3}\\
speed \hspace{1mm}=60 \div \frac{2}{3} = 90km/hr\)
Calculate and correct to two significant figures, the percentage error in approximating 0.375 to 0.4
2.0
2.5
6.6
6.7
Correct answer is D
Measured value = 0.375
Approximation = 0.4
Error = 0.4 - 0.375 = 0.025
Error% = \(\frac{0.025}{0.375}\) x 100% = 6.67% = 6.7%
WAEC Subjects
Aptitude Tests