Evaluate \(\frac{log8}{log\left(\frac{1}{4}\right)}\)
-2
\(\frac{-3}{2}\)
\(\frac{1}{2}\)
4
Correct answer is B
\(\frac{log8}{log\frac{1}{4}}=\frac{log2^3}{log2^{-2}}=\frac{3log2}{-2log2}=-\frac{3}{2}\)
Find the value of x which satisfies the equation
5(x-7)=7-2x
x =2
x=4
x=6
x = 14
Correct answer is C
5(x - 7) = 7 - 2x
5x - 35 = 7 - 2x
5x + 2x = 7 + 35
7x = 42
x = \(\frac{42}{7}\)
= 6
Simplify \(\left(1\frac{2}{3}\right)^2 - \left(\frac{2}{3}\right)^2\)
\(2\frac{1}{3}\)
\(1\frac{1}{3}\)
1
\(\frac{3}{7}\)
Correct answer is A
\(\left(1\frac{2}{3}\right)^2 - \left(\frac{2}{3}\right)^2=\left(\frac{5}{3}\right)^2 - \left(\frac{2}{3}\right)^2\)
Difference of two squares
\(\left(\frac{5}{3}-\frac{2}{3}\right)\left(\frac{5}{3}+\frac{2}{3}\right)=\left(\frac{3}{3}\right)\left(\frac{7}{3}\right)\\
\frac{7}{3}=2\frac{1}{3}\)
1
4
5
6
Correct answer is C
\(5+x\rightarrow 500\\
3 \rightarrow 150\\
∴ 3 \times 500 = 150 \times (5+x)\\
1500 = 750 + 150x\\
x=\frac{750}{150}=5\)
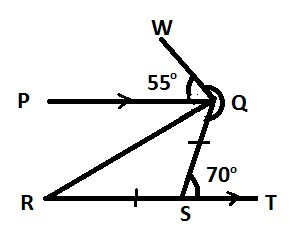
In the diagram, PQ/RT /RS/ =/QS/, ∠QST= 70° and ∠PQW = 55°
Find the size of reflex ∠WQS
235o
290o
305o
325o
Correct answer is A
Reflex ∠WQS = 360° - (55° + 70°)
=360° - 125° = 235°
WAEC Subjects
Aptitude Tests