3.4
4.3
5.9
6.2
Correct answer is B
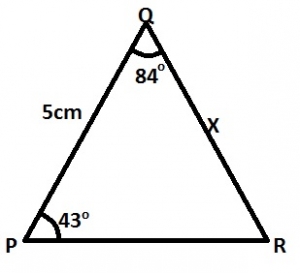
Using the sine rule
\frac{|QR|}{sinP}=\frac{|PQ|}{sinR}\\
\frac{x}{sin43^o}=\frac{5}{sin53^o}\\
x = \frac{5\times sin43^o}{sin53^o}\\
=\frac{5\times 0.6820}{0.7986}\\
=4.3
Find the value of x in the equation 3x^2 - 8x - 3 = 0
\frac{1}{3},-3
-\frac{1}{3},-3
-\frac{1}{3},3
\frac{1}{3},3
Correct answer is C
3x^2 - 8x - 3 = 0
3x^2 - 9x + x - 3 = 0
3x(x - 3) + 1(x - 3) = 0
(3x + 1)(x - 3) = 0
3x = -1 \implies x = -\frac{1}{3}
or x = 3.
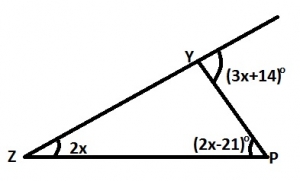
In the diagram, ZM is a straight line. Calculate the value of x.
27o
30o
35o
37o
Correct answer is C
The sum of angles in a triangle is 180o
2xo + (2x -21)o + ∠ZYP = 180o
Also ∠ZYP = 180o - (3x+14)o
∴2xo + (2x-21)o + 180o - (3x+14)o = 180
x = 35o
PQRS is a cyclic quadrilateral. If ∠QPS = 75°, what is the size of ∠QRS?
180o
150o
105o
75o
Correct answer is C
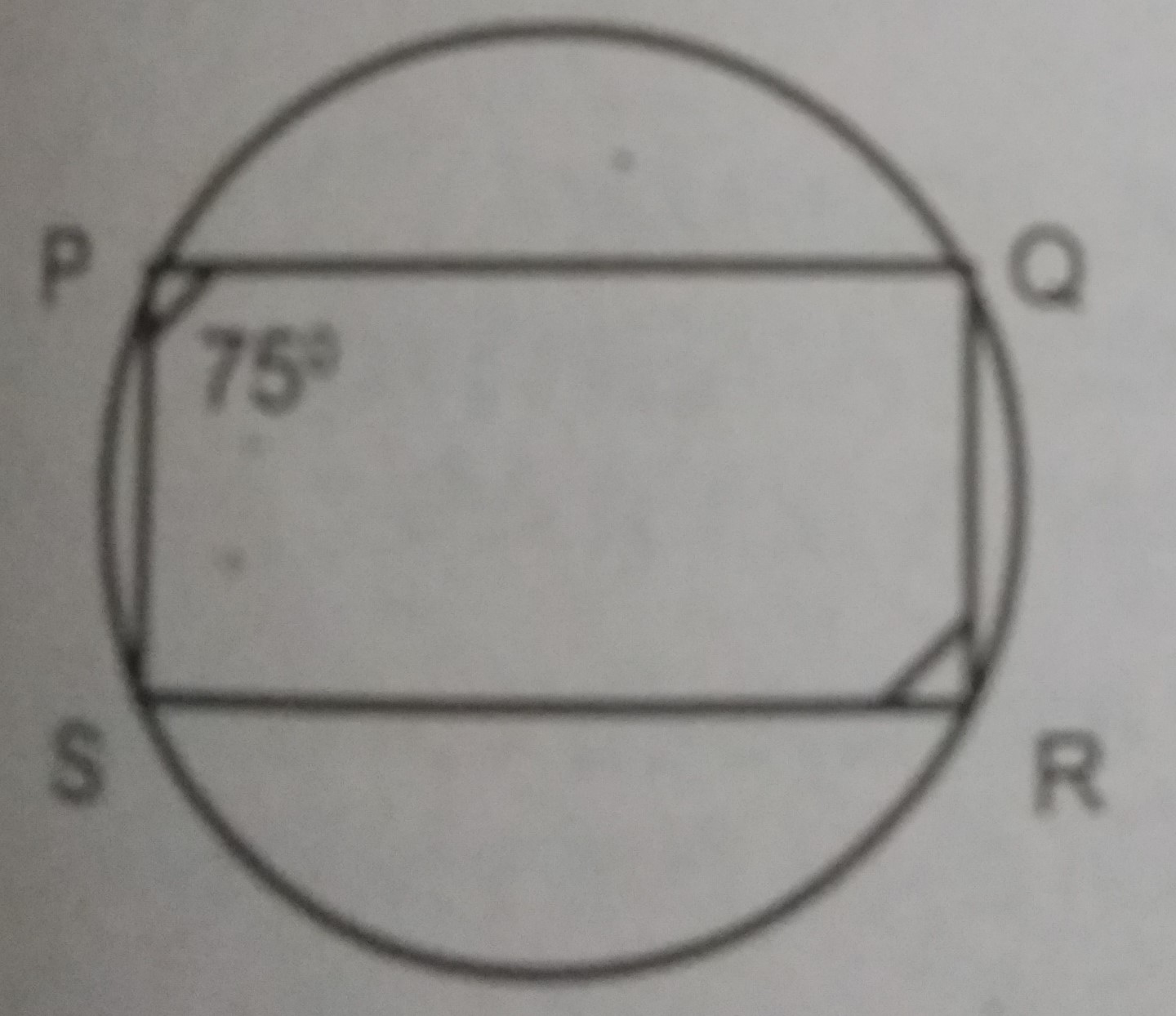
< QPS = 75°
< QRS = 180° - 75° = 105° (opposite angles of a cyclic quadrilateral)
5cm
9cm
12cm
15cm
Correct answer is C
V= \frac{1}{2}\hspace{1mm}base\hspace{1mm}area\hspace{1mm}\times\hspace{1mm}height\\ 120=\frac{1}{3}\times 5 \times 6 \times h; h = \frac{120}{10}=12cm
WAEC Subjects
Aptitude Tests