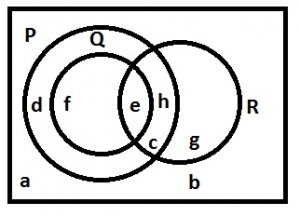
From the Venn diagram below, how many elements are in P∩Q?
1
2
4
6
Correct answer is B
P ∩ Q = {f, e} = 2
If P=√QR(1+3tR), make R the subject of the formula.
R=3QtP2−Q
R=P2–3tQ+1
R=P2+3tQ−1
R=P2−3QtQ
Correct answer is D
No explanation has been provided for this answer.
2√3
4√3
6√3
12√3
Correct answer is B
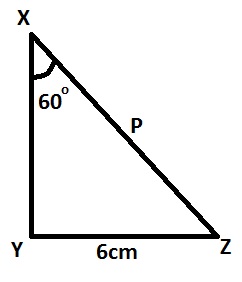
sinθ=opphypsin60o=|YZ||XZ|=6PPsin60o=6P=6sin60o=6√32=4√3
Which of the following is/are not the interior angle(s) of a regular polygon?
I.108°
II. 116°
III. 120°
I only
II only
III only
I and III only
Correct answer is B
Using the formula, (n - 2) \times 180° to get the sum of the interior angles. Then we can have
(n - 2) \times 180° = 108n ... (1)
(n - 2) \times 180° = 116n ... (2)
(n - 2) \times 180° = 120n ... (3)
Solving the above given equations, where n is not a positive integer then that angle is not the interior for a regular polygon.
(1): 180n - 360 = 108n \implies 72n = 360
n = 5 (regular pentagon)
(2): 180n - 360 = 116n \implies 64n = 360
n = 5.625
(3): 180n - 360 = 120n \implies 60n = 360
n = 6 (regular hexagon)
Hence, 116° is not an angle of a regular polygon.
If \frac{3^{(1-n)}}{9^{-2n}}=\frac{1}{9} find n
-\frac{3}{2}
\frac{1}{3}
-1
-3
Correct answer is C
\frac{3^{(1-n)}}{9^{-2n}}=\frac{1}{9}\\ 3^{1-n}\times 3^{-2(-2n)} = 3^{-2}\\ 1-n-2(-2n)= -2\\ 1-n+4n=-2\\ n=-1
WAEC Subjects
Aptitude Tests