34cm
52cm
56cm
96cm
Correct answer is B
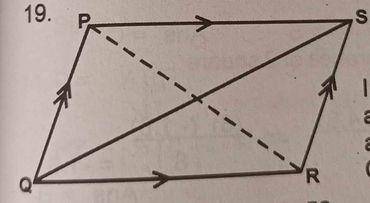
For a rhombus, all the sides are equal and diagonals bisect each other at 90o. Hence, the triangles formed are congruent: (under RHS).
Thus: ¯PS2 = 52 + 122
¯PS=√25+144
= √169
¯PS = 13cm
perimeter = 4 x length of a side
= 4 x 13cm
= 52cm
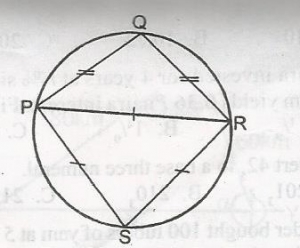
In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS
150o
120o
90o
60o
Correct answer is C
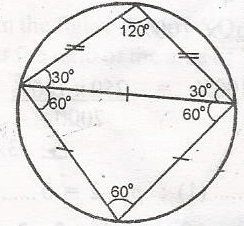
Since |PR| = |RS| = |SP|
△ PRS is equilateral and so < RPS = < PRS = < PSR = 70o
But < PQR + < PSR = 180o (Opposite interior angles of a cyclic quadrilateral)
< PQR + 60 = 180o
< PR = 180 - 60 = 120o
But in △ PQR, PQ = PR, hence < QPR = < PRQ(Base angles of an Isosceles triangle)
< QPR + < PRQ + < PQR = 180o (Angles in a triangle)
2 < QPR + 120 = 18-
2 < QPR = 180 - 120
QPR = 602 = 30o
From the diagram, < QRS = < PRQ + < PRS
30 + 60 = 90o
1
34
14
zero
Correct answer is D
x2359246101848122036612183054816244072
Note: A {horizontal}
B {vertical}
Pr (Odd Product) = 016
= 0
WAEC Subjects
Aptitude Tests