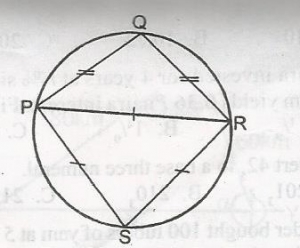
In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS
150o
120o
90o
60o
Correct answer is C
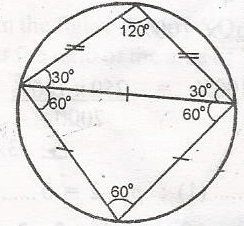
Since |PR| = |RS| = |SP|
△ PRS is equilateral and so < RPS = < PRS = < PSR = 70o
But < PQR + < PSR = 180o (Opposite interior angles of a cyclic quadrilateral)
< PQR + 60 = 180o
< PR = 180 - 60 = 120o
But in △ PQR, PQ = PR, hence < QPR = < PRQ(Base angles of an Isosceles triangle)
< QPR + < PRQ + < PQR = 180o (Angles in a triangle)
2 < QPR + 120 = 18-
2 < QPR = 180 - 120
QPR = 602 = 30o
From the diagram, < QRS = < PRQ + < PRS
30 + 60 = 90o
Similar Questions
Solve for the equation √x - √(x−2) - 1 = 0...
Evaluate \(\begin{vmatrix} 2 & 0 & 5 \\ 4 & 6 & 3 \\ 8 & 9 & 1 \end{vmatrix}...
If sinθ=1213, find the value of 1+cosθ...
Simplify 2.04 × 3.7 (Leave your answer in 2 decimal place) ...
Find the equation of a line perpendicular to line 2y = 5x + 4 which passes through (4, 2). ...
In the diagram above, O is the center of the circle PQRS and ∠QPS = 36°. Find ∠QOS ...
Find the values of p and q such that (x - 1)and (x - 3) are factors of px3 + qx2 + 11x - 6 ...