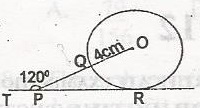
2.32cm
1.84cm
0.62cm
0.26cm
Correct answer is C
No explanation has been provided for this answer.
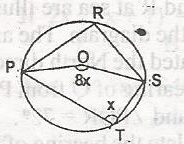
The diagram is a circle with centre P. PRST are points on the circle. Find the value of < PRS
144o
72o
40o
36o
Correct answer is A
Reflex < POS = 2x (angle at centre is twice that at circumference)
reflex < POS + < POS = 350o(angles at a point)
i.e. 2x + 8x = 360o
10x = 360o
x = \(\frac{360}{10}\)
= 36o
< PRS = \(\frac{1}{2}\)
< POS(< at centre twice that circumference)
= \(\frac{1}{2}\) x 8x = 4x
4 x 36o
< PRS = 144
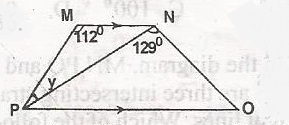
In the diagram, MN//PO, < PMN = 112o, < PNO = 129oo and < MPN = yo. Find the value of y
51o
54o
56o
68o
Correct answer is B
In \(\bigtriangleup\) NPO + PNO + PNO + < NOP = 180o(sum of interior angles of a \(\bigtriangleup\) )
i.e. NPO + 129 + 37 = 180
< NOP = 180 - (129 + 37) = 14o
< MNP = < NOP = 14o (alt. < s)
In \(\bigtriangleup\) MPN
< PMN + < MNP + y = 180(sum of interior angles of a \(\bigtriangleup\))
i.e. 112 + 14 + y = 180o
y = 180 - (112 + 14) = 180 - 126 = 54o
11.1
10.5
10.3
9.9
Correct answer is A
No explanation has been provided for this answer.
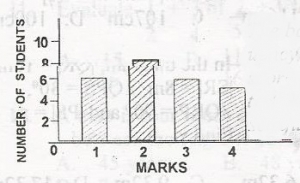
2
4
6
8
Correct answer is A
median = (\(\frac{N + 1}{2}\))th = (\(\frac{25 + 1}{2}\))th
= \(\frac{26th}{2}\)
= 13th
the 13th is 2
WAEC Subjects
Aptitude Tests