\(\frac{5}{6}\)
\(\frac{7}{12}\)
\(\frac{5}{12}\)
\(\frac{1}{6}\)
Correct answer is C
let the girls' initial pocket money be whole(1)
\(\frac{1}{4}\) of 1 = books, \(\frac{1}{3}\) of 1 = dress
fraction of her money left = 1 - \(\frac{1}{4}\) - \(\frac{1}{3}\)
= \(\frac{5}{12}\)
Solve for t in the equation \(\frac{3}{4}\)t + \(\frac{1}{3}\)(21 - t) = 11
\(\frac{9}{13}\)
\(\frac{7}{13}\)
5
9\(\frac{3}{5}\)
Correct answer is D
\(\frac{3}{4}\) t + \(\frac{1}{3}\) (21 - t) = 11
Multiply through by the LCM of 4 and 3 which is 12
12 x(\(\frac{3}{4}\) t) + 12 x (\(\frac{1}{3}\) (21 - t)) = (11 x 12)
9t + 4(21 - t) = 132
9t + 84 - 4t = 132
5t + 84 = 132
5t = 132 - 84 = 48
t = \(\frac{48}{5}\)
t = 9 \(\frac{3}{5}\)
Answer is D
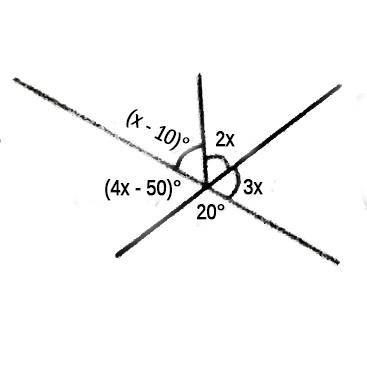
Find the value of x in the diagram
10°
28°
36°
40°
Correct answer is D
The diagram shows angles at a point, the total angle at a point is 360
x - 10 + 4x - 50 + 2x + 3x + 20 = 360
10x - 40 = 360
10x = 360 + 40
10x = 400
x = \(\frac{400}{10}\)
x = 40
If y = 23\(_{five}\) + 101\(_{three}\) , find y, leaving your answer in base two
1110
10111
11101
111100
Correct answer is B
y = 23\(_{five}\) + 101\(_{three}\)
23\(_{five}\) = \(2 \times 5^1 + 3 \times 5^0\)
= 13\(_{ten}\)
101\(_{three}\) = \(1 \times 3^2 + 0 \times 3^1 + 1 \times 3^0\)
= 10\(_{ten}\)
y\(_{ten}\) = 13\(_{ten}\) + 10\(_{ten}\)
= 23\(_{ten}\)
= 10111\(_{two}\)
If y = 23\(_{five}\) + 101\(_{three}\) , find y, leaving your answer in base two
1110
10111
11101
111100
Correct answer is B
y = 23\(_{five}\) + 101\(_{three}\)
23\(_{five}\) = \(2 \times 5^1 + 3 \times 5^0\)
= 13\(_{ten}\)
101\(_{three}\) = \(1 \times 3^2 + 0 \times 3^1 + 1 \times 3^0\)
= 10\(_{ten}\)
y\(_{ten}\) = 13\(_{ten}\) + 10\(_{ten}\)
= 23\(_{ten}\)
= 10111\(_{two}\)
JAMB Subjects
Aptitude Tests