3150
2031
3120
5031
Correct answer is D
23÷4514+35−13
23÷45=23×54
= 56
14+35−13=15+36−2060
= 3160
∴
= \frac{5}{6} \times \frac{60}{31}
= \frac{50}{31}
Given \sin 58° = \cos p°, find p.
48°
58°
32°
52°
Correct answer is C
\sin \theta = \cos (90 - \theta)
\sin \theta = \cos (90 - 58)
= \cos 32
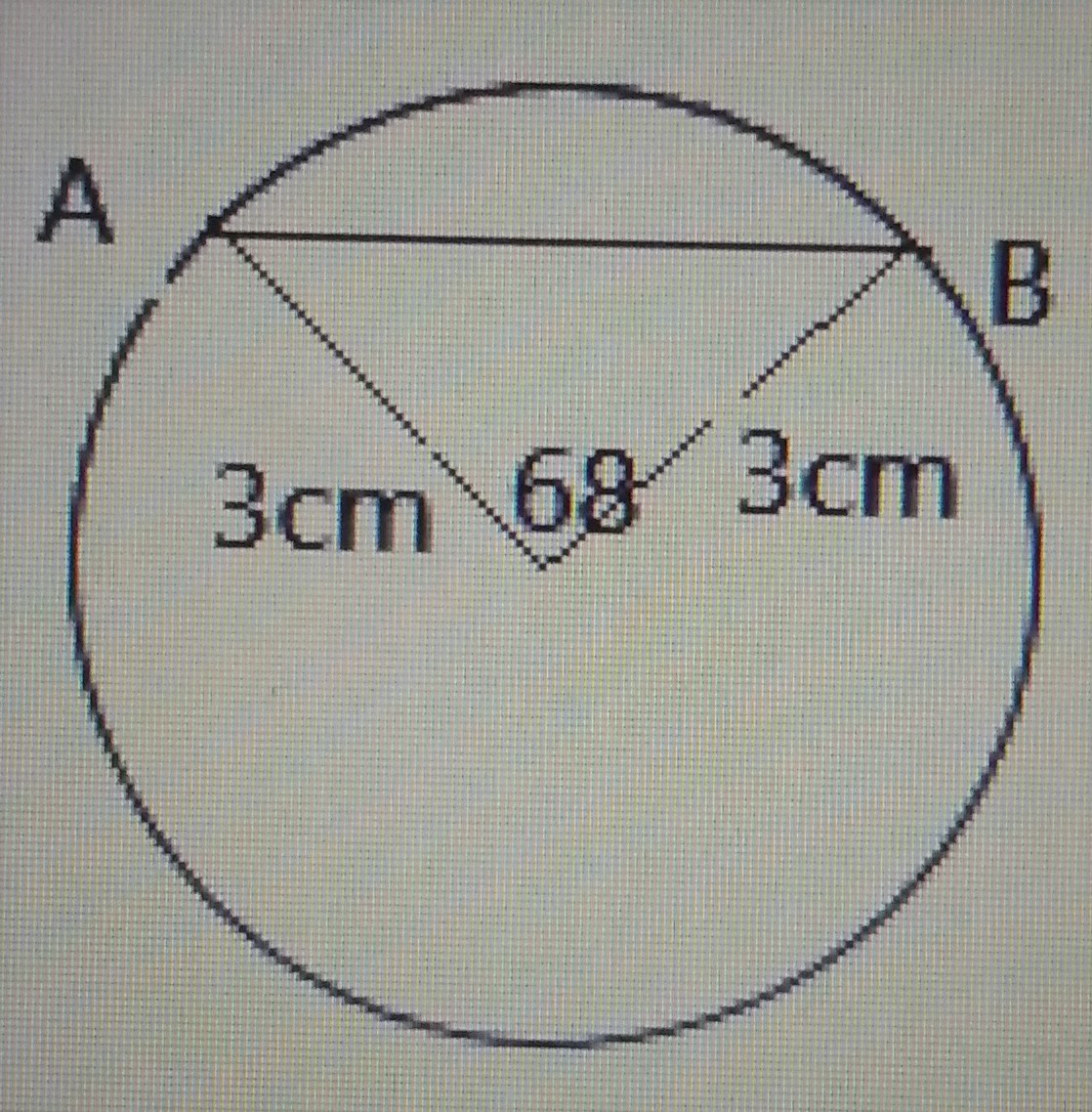
Find the length of the chord |AB| in the diagram shown above.
4.2 cm
4.3 cm
3.2 cm
3.4 cm
Correct answer is D
Length of chord = 2r \sin (\frac{\theta}{2})
= 2(3) \sin (\frac{68}{2})
= 6 \sin 34
= 6 \times 0.559
= 3.354 cm \approxeq 3.4 cm
Rationalize \frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}}
-5 - 2\sqrt{6}
-5 + 3\sqrt{2}
5 - 2\sqrt{3}
5 + 2\sqrt{6}
Correct answer is A
\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}}
= (\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} - \sqrt{3}})(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{2} + \sqrt{3}})
= \frac{2 + \sqrt{6} + \sqrt{6} + 3}{2 - \sqrt{6} + \sqrt{6} - 3}
= \frac{5 + 2\sqrt{6}}{-1}
= - 5 - 2\sqrt{6}
42
20
70
54
Correct answer is B
n(Total) = 50
n(Physics) = 40
n(Biology) = 30
Let n(Physics and Biology) = x
n(Physics only) = 40 -x
n(Biology only) = 30 - x
40 - x + 30 - x + x = 50
70 - x = 50
x = 20
JAMB Subjects
Aptitude Tests