
PQRS is a cyclic quadrilateral. Find \(x\) + \(y\)
50
60
15
0
Correct answer is D
∠PQR + ∠PSR = 180o (opp. angles of cyclic quad. are supplementary)
⇒ 5\(x\) - \(y\) + 10 + (-2\(x\) + 3\(y\) + 145) = 180
⇒ 5\(x\) - \(y\) + 10 - 2\(x\) + 3\(y\) + 145 = 180
⇒ 3\(x\) + 2\(y\) + 155 = 180
⇒ 3\(x\) + 2\(y\) = 180 - 155
⇒ 3\(x\) + 2\(y\) = 25 ----- (i)
∠QPS + ∠QRS = 180o (opp. angles of cyclic quad. are supplementary)
⇒ -4\(x\) - 7\(y\) + 150 + (2\(x\) + 8\(y\) + 105) = 180
⇒ -4\(x\) - 7\(y\) + 75 + 2\(x\) + 8\(y\) + 180 = 180
⇒ -2\(x\) + \(y\) + 255 = 180
⇒ -2\(x\) + y = 180 - 255
⇒ -2\(x\) + \(y\) = -75 ------- (ii)
⇒ \(y\) = -75 + 2\(x\) -------- (iii)
Substitute (-75 + 2\(x\)) for \(y\) in equation (i)
⇒ 3\(x\) + 2(-75 + 2\(x\)) = 25
⇒ 3\(x\) - 150 + 4\(x\) = 25
⇒ 7\(x\) = 25 + 150
⇒ 7\(x\) = 175
⇒ \(x = \frac{175}{7} = 25\)
From equation (iii)
⇒ \(y\) = -75 + 2(25) = -75 + 50
⇒ \(y\) = -25
∴ \(x\) + \(y\) = 25 + (-25) = 0
10 cm and 15 cm
8 cm and 12 cm
6 cm and 9 cm
12 cm and 18 cm
Correct answer is A

Area of trapezium = \(\frac{1}{2}(a + b) h\)
⇒ \(\frac{1}{2} (a + b)\times 16 = 200\)
⇒ 8(a + b) = 200
⇒ a + b = \(\frac{200}{8}\) = 25 -----(i)
⇒ a : b = 2 : 3
⇒ \(\frac{a}{b} = \frac{2}{3}\)
⇒ 3a = 2b
⇒ a = \(\frac{2b}{3}\) -------(ii)
Substitute \(\frac{2b}{3}\) for a in equation (i)
⇒ \(\frac{2b}{3}\) + b = 25
\(\frac{5b}{3}\) = 25
⇒ b = 25 ÷ \(\frac{5}{3} = 25\times\frac{3}{5} = 15cm\)
From equation (ii)
⇒ a = \(\frac{2 \times 15}{3} = 2\times5 = 10cm\)
∴ Lengths of each parallel sides are 10cm and 15cm

380
340
360
240
Correct answer is C
Total number of students that scored at most 50 marks = 100 + 80 + 60 + 40 + 80 = 360
Find the volume of a cone which has a base radius of 5 cm and slant height of 13 cm.
\(300\pi\) cm\(^3\)
\(325\pi\) cm\(^3\)
\(\frac{325}{3}\pi\) cm\(^3\)
\(100\pi\) cm\(^3\)
Correct answer is D

Volume of a cone = \(\frac{1}{3}\pi r^2 h\)
r = 5 cm
l = 13 cm
Using Pythagoras theorem
⇒ \(13^2 = 5^2 + h^2\)
⇒ \(169 = 25 + h^2\)
⇒ \(169 - 25 = h^2\)
⇒ \(h^2 = 144\)
⇒ \(h = \sqrt144 = 12 cm\)
∴ Volume of the cone = \(\frac{1}{3} \times\pi\times 5^2 x 12 = 100\pi\) cm\(^3\)
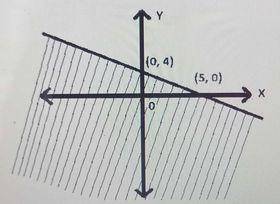
Which inequality describes the graph above?
\(4y + 5x ≥ 20\)
\(5y + 4x ≤ 20\)
\(4y + 5x ≤ 20\)
\(5y + 4x ≥ 20\)
Correct answer is B
First, we find the equation of the boundary line using the two intercepts.The slope is
m = \(\frac{4 - 0}{0 - 5} = {4}{5}\)
The y-intercept is 4
The slope-intercept form of the equation is therefore
y = -\(\frac{4}{5} x + 4\)
\(\implies y + \frac{4}{5} x = 4\)
Multiply both sides by \(\frac{5}{4}\)
\(\implies\frac{5}{4}(y +\frac{4}{5} x) = 4\times\frac{5}{4}\)
\(\implies\frac{5}{4} y + x = 5\)
Multiply both sides by 4
⇒ \(5y + 4x = 20\)
The inequality is therefore either \(5y + 4x ≤ 20\) or \(5y + 4x ≥ 20.\)
Using the test point (0, 0) -The origin
⇒ 5(0) + 4(0) ≤ 20
⇒ 0 ≤ 20 (True)
∴ The inequality is \(5y + 4x ≤ 20\)
JAMB Subjects
Aptitude Tests