Divide 1101001\(_{two}\) by 101\(_{two}\)
11101\(_{two}\)
111\(_{two}\)
10111\(_{two}\)
10101\(_{two}\)
Correct answer is D

No explanation has been provided for this answer.
2 hrs
4 hrs
3 hrs3 hrs
1 hr
Correct answer is C
Let T be the time taken and D is the distance
For the case given in the problem, the distance covered is directly proportional to the time taken i.e D α T
⇒ D = ST where S is the constant speed
D = 225 km and T = 4.5 hrs
∴ 225 = S x 4.5
S = \(\frac {225}{4.5}\) = 50km/hr
When D = 150km
D = ST
150 = 50 \(\times\) T
T = \(\frac {150}{50}\) = 3 hrs
So it will take 3 hrs
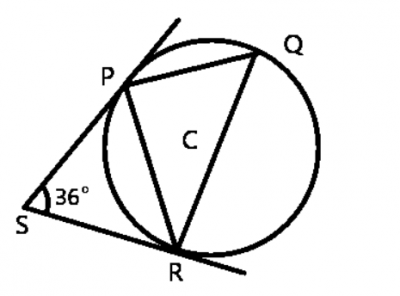
72\(^0\)
36\(^0\)
144\(^0\)
54\(^0\)
Correct answer is A
From ∆PSR
|PS| = |SR| (If two tangents are drawn from an external point of the circle, then they are of equal lengths)
∴ ∆PSR is isosceles
∠PSR + ∠SRP + ∠SPR = 180\(^o\) (sum of angles in a triangle)
Since |PS| = |SR|; ∠SRP = ∠SPR
⇒ ∠PSR + ∠SRP + ∠SRP = 180\(^o\)
∠PSR + 2∠SRP = 180\(^o\)
36\(^o\) + 2∠SRP = 180\(^o\)
2∠SRP = 180\(^o\) - 36\(^o\)
2∠SRP = 144\(^o\)
∠SRP = \(\frac {144^o}{2} = 72^0\)
∠SRP = ∠PQR (angle formed by a tangent and chord is equal to the angle in the alternate segment)
∴ ∠PQR = 72\(^0\)
Solve for x: 3(x – 1) ≤ 2 (x – 3)
x ≤ -3
x ≥ -3
x ≤ 3
x ≥ 3
Correct answer is A
3(x – 1) ≤ 2 (x – 3)
= 3x – 3 ≤ 2x – 6
Add 3 to both sides
= 3x – 3+ 3 ≤ 2x – 6+ 3
= 3x ≤ 2x – 3
Subtract 2x from both the sides
= 3x – 2x ≤ 2x – 3 – 2x
∴ x ≤ -3
Make x the subject of the formula:y = \(\frac {3x - 9c}{4x + 5d}\)
x = \(\frac {(-9c - 5dy)}{4y - 3}\)
x = \(\frac {-9c + 5dy}{4y - 3}\)
x = \(\frac {(-9c + 5dy)}{4y - 3}\)
x = \(\frac {-(9c + 5dy)}{4y - 3}\)
Correct answer is D
y = \(\frac {3x - 9c}{4x + 5d}\)
\(\frac {y}{1} = \frac {3x - 9c}{4x + 5d}\)
= y(4x + 5d) = 3x - 9c
= 4xy + 5dy = 3x - 9c
= 4xy - 3x = -9c - 5dy
= (4y - 3)x = -9c - 5dy
= x = \(\frac {-9c - 5dy}{4y - 3}\)
x = \(\frac {-(9c + 5dy)}{4y - 3}\)
JAMB Subjects
Aptitude Tests