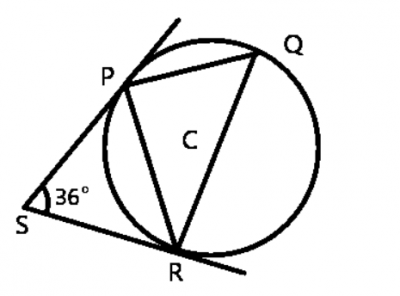
The diagram above is a circle with centre C. P, Q and S are points on the circumference. PS and SR are tangents to the circle. ∠PSR = 36o. Find ∠PQR
720
360
1440
540
Correct answer is A
From ∆PSR
|PS| = |SR| (If two tangents are drawn from an external point of the circle, then they are of equal lengths)
∴ ∆PSR is isosceles
∠PSR + ∠SRP + ∠SPR = 180o (sum of angles in a triangle)
Since |PS| = |SR|; ∠SRP = ∠SPR
⇒ ∠PSR + ∠SRP + ∠SRP = 180o
∠PSR + 2∠SRP = 180o
36o + 2∠SRP = 180o
2∠SRP = 180o - 36o
2∠SRP = 144o
∠SRP = 144o2=720
∠SRP = ∠PQR (angle formed by a tangent and chord is equal to the angle in the alternate segment)
∴ ∠PQR = 720
Similar Questions
If x - 3 is directly proportional to the square of y and x = 5 when y =2, find x when y = 6. ...
Given that p:q = 13:12 and q:r = 25, find p:r...
Find P, if 4516 - P7 = 3056 ...
An arc of circle of radius 2cm subtends an angle of 60º at the centre. Find the area of th...