3\(\sqrt{2}\)
2\(\sqrt{3}\)
\(\frac{\sqrt{3}}{2}\)
\(\frac{2}{\sqrt{3}}\)
Correct answer is B
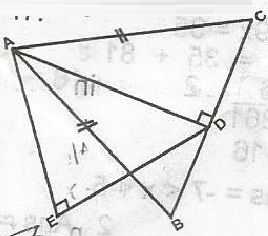
BC = 6 : DC = \(\frac{6}{2}\) = 3cm
By construction < EDE = 180o(90o + 60o) = 180o - 150o
= 30o(angle on a strt. line)
From rt < triangle ADC, AD2 = 52 - 32
= 25 - 9 = 6
AD = 4
From < AEC, let AS = x
\(\frac{x}{sin 60^o}\) - \(\frac{4}{sin 90^o}\)
sin 90o = 1
sin 60o = \(\frac{\sqrt{3}}{2}\)
x = 4sin 60o
x = 3 x \(\frac{\sqrt{3}}{2}\)
= 2\(\sqrt{3}\)
70o
110o
130o
125o
145o
Correct answer is D
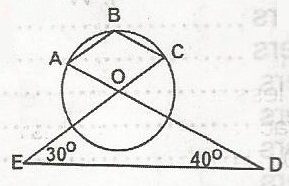
If < CED = 30º, and < EDA = 40º then
<EOD = 180-(30-40) (angles in a triangle sum to 180) → 110º
<AOC = <EOD = 110º
At centre O: 360 - 110 = 250º
The angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference.
250 * \(\frac{1}{2}\) → 125º
<ABC = 125º
\(\sqrt{33}\)
6
4
2\(\sqrt{13}\)
4\(\sqrt{5}\)
Correct answer is D
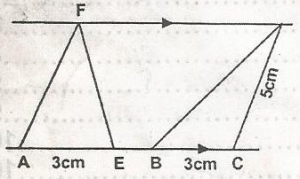
Area of triangle AEF = 6sq. cm
area of triangle = \(\frac{1}{2}\)bh (Line DX makes right angles with the parallel lines)
6 = \(\frac{1}{2}\) x 3 x h
6 = 3h
3h = \(\frac{12}{3}\)
h = 4 = DX
From D, C x D, CX2 = 52
- 42
= 25 - 16 = 9
Cx = 3. From angle B x D, Bx = 6(i.e. 3 + 3)
BD2 = 42 + 62
= 16 + 36 = 52
BD = \(\sqrt{4 \times 13}\)
= 2\(\sqrt{13}\)
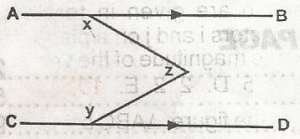
In the figure, AB is parallel to CD then x + y + z is
185o
200o
270o
360o
195o
Correct answer is D
x + y + z = 360o
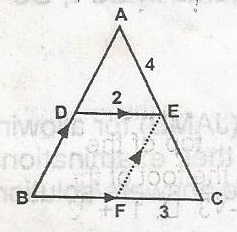
In the figure, DE//BC: DB//FE: DE = 2cm, FC = 3cm, AE = 4cm. Determine the length of EC.
4cm
6cm
3cm
2cm
1cm
Correct answer is B
Angles ADE and EFC are similar,
Therefore,
= \(\frac{x}{3} = \frac{4}{2}\)
= \(\frac{x}{3} = 2\)
x = 3 x 2 = 6
JAMB Subjects
Aptitude Tests