In the figure, \(\bigtriangleup\) ABC are in adjacent pla...
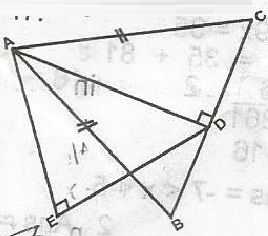
In the figure, \(\bigtriangleup\) ABC are in adjacent planes. AB = AC = 5cm, BC = 6cm and o then AE is equal to
3\(\sqrt{2}\)
2\(\sqrt{3}\)
\(\frac{\sqrt{3}}{2}\)
\(\frac{2}{\sqrt{3}}\)
Correct answer is B
BC = 6 : DC = \(\frac{6}{2}\) = 3cm
By construction < EDE = 180o(90o + 60o) = 180o - 150o
= 30o(angle on a strt. line)
From rt < triangle ADC, AD2 = 52 - 32
= 25 - 9 = 6
AD = 4
From < AEC, let AS = x
\(\frac{x}{sin 60^o}\) - \(\frac{4}{sin 90^o}\)
sin 90o = 1
sin 60o = \(\frac{\sqrt{3}}{2}\)
x = 4sin 60o
x = 3 x \(\frac{\sqrt{3}}{2}\)
= 2\(\sqrt{3}\)
Similar Questions
Simplify 0.000215 x 0.000028 and express your answer in standard form ...
Find the minimum value of y = x2 - 2x - 3...
Calculate, correct to three significant figures, the length AB in the diagram above. ...
Find the value of m in the diagram ...
Evaluate log5(\( y^2x^5 ÷ 125b½) \)...
Three boys shared D 10,500.00 in the ratio 6:7:8. Find the largest share. ...