In the Figure FD\\AC, the area of AEF = 6sq.cm. AE = 3cm,...
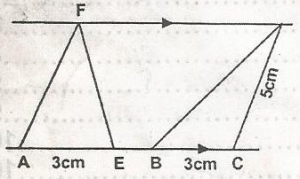
In the Figure FD\\AC, the area of AEF = 6sq.cm. AE = 3cm, BC = 3cm, CD = 5cm, < BCD is an obtuse angle. Find the length of BD.
√33
6
4
2√13
4√5
Correct answer is D
Area of triangle AEF = 6sq. cm
area of triangle = 12bh (Line DX makes right angles with the parallel lines)
6 = 12 x 3 x h
6 = 3h
3h = 123
h = 4 = DX
From D, C x D, CX2 = 52
- 42
= 25 - 16 = 9
Cx = 3. From angle B x D, Bx = 6(i.e. 3 + 3)
BD2 = 42 + 62
= 16 + 36 = 52
BD = √4×13
= 2√13
Similar Questions
The graph of the quadratic expression ...
Evaluate (20three)2−(11three)2 in base three...
The volume of a cone (s) of height 6cm and base radius 5cm is ...
Find the value of tan60o−tan30otan60o+tan30o ...
What is the place value of 9 in the number 3.0492? ...