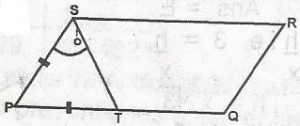
In this figure, PQRS is a parallelogram, PS = PT and < PST = 55o. The size of <PQR is
125o
120o
115o
110o
10o
Correct answer is D
Both pairs of opp. angles are equal
< STP = 55o - isosceles angle
< TSR = 55o - alternate angle to < STP
Hence, < PSR = 55o + 55o = 110o
∴ < PQR = 110^o
3\sqrt{2}
2\sqrt{3}
\frac{\sqrt{3}}{2}
\frac{2}{\sqrt{3}}
Correct answer is B
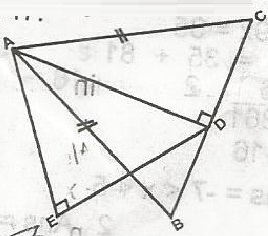
BC = 6 : DC = \frac{6}{2} = 3cm
By construction < EDE = 180o(90o + 60o) = 180o - 150o
= 30o(angle on a strt. line)
From rt < triangle ADC, AD2 = 52 - 32
= 25 - 9 = 6
AD = 4
From < AEC, let AS = x
\frac{x}{sin 60^o} - \frac{4}{sin 90^o}
sin 90o = 1
sin 60o = \frac{\sqrt{3}}{2}
x = 4sin 60o
x = 3 x \frac{\sqrt{3}}{2}
= 2\sqrt{3}
70o
110o
130o
125o
145o
Correct answer is D
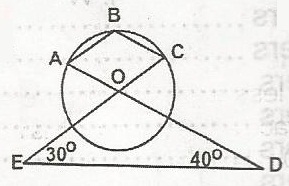
If < CED = 30º, and < EDA = 40º then
<EOD = 180-(30-40) (angles in a triangle sum to 180) → 110º
<AOC = <EOD = 110º
At centre O: 360 - 110 = 250º
The angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference.
250 * \frac{1}{2} → 125º
<ABC = 125º
\sqrt{33}
6
4
2\sqrt{13}
4\sqrt{5}
Correct answer is D
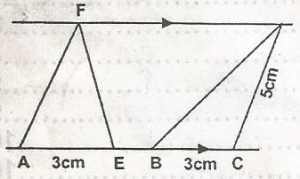
Area of triangle AEF = 6sq. cm
area of triangle = \frac{1}{2}bh (Line DX makes right angles with the parallel lines)
6 = \frac{1}{2} x 3 x h
6 = 3h
3h = \frac{12}{3}
h = 4 = DX
From D, C x D, CX2 = 52
- 42
= 25 - 16 = 9
Cx = 3. From angle B x D, Bx = 6(i.e. 3 + 3)
BD2 = 42 + 62
= 16 + 36 = 52
BD = \sqrt{4 \times 13}
= 2\sqrt{13}
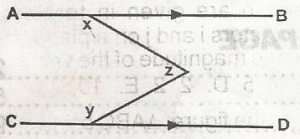
In the figure, AB is parallel to CD then x + y + z is
185o
200o
270o
360o
195o
Correct answer is D
x + y + z = 360o
JAMB Subjects
Aptitude Tests