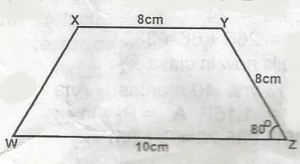
In the figure, find the area of XYZW
60cm2
54cm2
36cm2
54\(\sqrt{2}\)cm2
27\(\sqrt{2}\)cm2
Correct answer is C
Average of trapezium XYZW = \(\frac{1}{2}\)(a + b)h from rt < YDZ,
h = 8 sin 30º
area = \(\frac{1}{2}\)(10 + 8)4
= 8 x \(\frac{1}{2}\) = 4
\(\frac{1}{2}\)(18) x 4
= 36cm2
50o
75o
35o
115o
30o
Correct answer is C
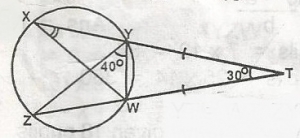
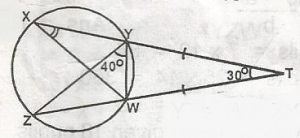
< WYT = \(\frac{180 - 30}{2}\)
= \(\frac{150}{2}\)
= 75o(base angles of isosceles D)
YXW = 75 - 40 = 35o(Exterior angle is equal to sum of interior angles)
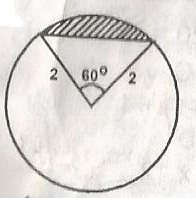
Find the area of the shades segments in the figure
\(\sqrt{3}\)
4 \(\pi - \sqrt{3}\)
-\(\frac{2}{3} \pi\)
\(\frac{2\pi}{3}\) -3
Correct answer is D
Area of section = \(\frac{60^o}{360^o}\) x 11r2
= \(\frac{60}{360} \times \pi \times 2^2\)
= \(\frac{1}{6}\) x 4
= \(\frac{4\pi}{6}\)
= \(\frac{2\pi}{3}\)
Area of triangle = \(\frac{1}{2x}\)
= 2 x 28.......60
Segment Area = Area of section - Area of triangle
= \(\frac{2\pi}{3}\) -3
\(\frac{1}{2}\)
\(\frac{4}{\sqrt{3}}\)
\(\sqrt{3}\)
4\(\sqrt{3}\)
Correct answer is B
No explanation has been provided for this answer.
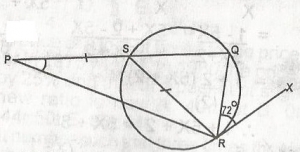
In the figure, PS = SR and Rx is a tangent to the circle at R, < QRX is equal to 72o. Find angle SPR
20o
36o
72o
30o
15o
Correct answer is B
XRQ = RSQ (Alternate segment)
s = 72o
(80o - 72o = 180o)
a + b + c = 190o = 2b + c = 180o
2b + 108 = 180o
2b = 72o
b = 36o
JAMB Subjects
Aptitude Tests