Find the area of the shades segments in the figure
...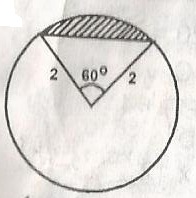
Find the area of the shades segments in the figure
\(\sqrt{3}\)
4 \(\pi - \sqrt{3}\)
-\(\frac{2}{3} \pi\)
\(\frac{2\pi}{3}\) -3
Correct answer is D
Area of section = \(\frac{60^o}{360^o}\) x 11r2
= \(\frac{60}{360} \times \pi \times 2^2\)
= \(\frac{1}{6}\) x 4
= \(\frac{4\pi}{6}\)
= \(\frac{2\pi}{3}\)
Area of triangle = \(\frac{1}{2x}\)
= 2 x 28.......60
Segment Area = Area of section - Area of triangle
= \(\frac{2\pi}{3}\) -3
Similar Questions
In the diagram, O is the centre of the circle where OS//QR and ∠SOR = 35o...
Calculate the mean deviation of 5, 3, 0, 7, 2, 1 ...
Given that A = {3, 4, 1, 10, ⅓ } B = {4, 3,⅓, ⅓, 7}. Find A∩B...
Factorize m(2a-b)-2n(b-2a) ...
If \(P344_{6} - 23P2_{6} = 2PP2_{6}\), find the value of the digit P. ...
lf sin θ= \(\frac{-1}{2}\), find all the values of θ between 0° and 360°....
On a pie chart there are six sectors of which four angles are 30°, 45°, 60°, 90°&nbs...