16cm
14cm
12cm
8cm
Correct answer is A
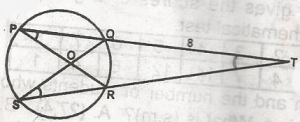
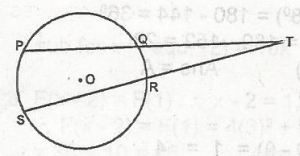
PT x QT = TR x TS
24 x 8 = TR x 12
TR = \(\frac{24 \times 8}{12}\)
= = 16cm
100o
120o
60o
110o
140o
Correct answer is E
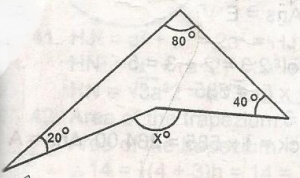
In the figure, angle x = 20o + 80o + 40o
= 140o
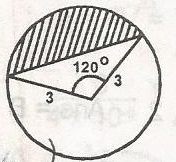
In the figure, the area of the shaded segment is
3\(\pi\)
9\(\frac{\sqrt{3}}{4}\)
3 \(\pi - 3 \frac{\sqrt{3}}{4}\)
\(\frac{(\sqrt{3 - \pi)}}{4}\)
\(\pi + \frac{9 \sqrt{3}}{4}\)
Correct answer is C
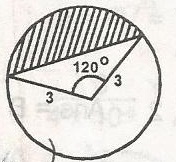
Area of sector = \(\frac{120}{360} \times \pi \times (3)^2 = 3 \pi\)
Area of triangle = \(\frac{1}{2} \times 3 \times 3 \times \sin 120^o\)
= \(\frac{9}{2} \times \frac{\sqrt{3}}{2} = \frac{9\sqrt {3}}{4}\)
Area of shaded portion = 3\(\pi - \frac{9\sqrt {3}}{4}\)
= 3 \(\pi - 3 \frac{\sqrt{3}}{4}\)
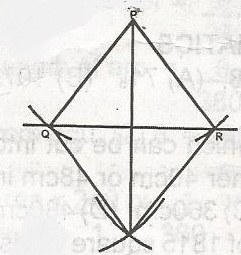
The figure is an example of the construction of a
perpendicular bisector of a given straight line QR
perpendicular from a given point to a given line QR
perpendicular to a line from a given point P on that line
given angle
Correct answer is B
QR is a given line and P is a given point. The construction is the perpendicular from a given point P to a given line QR
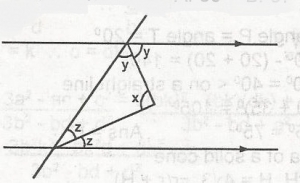
In the figure, find the value of x
110o
100o
90o
80o
Correct answer is C
Z = X = Y = 180o .........(i)
2Z + Y + Y = 190 = 2Z + 2Y = 180
Z + Y = 90o........(ii)
hence x + (z + y) = 180
x + 90o = 180o
x = 180o - 90o
= 90o
JAMB Subjects
Aptitude Tests