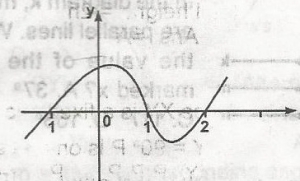
Use the graph of the curve y = f(x)to solve the inequality f(x) \(\leq\) 0
-1 \(\geq\) x \(\geq\) 1, x \(\geq\) 2
x \(\leq\) -1, 1 \(\geq\) x \(\geq\) 2
x \(\geq\) -1, 1 \(\geq\) x \(\geq\) 2
x \(\geq\) 2, -1 \(\geq\) x \(\geq\) 1
Correct answer is B
-1 \(\geq\) x \(\geq\) 1, 1 < x \(\geq\) 2
Combining solutions
= x \(\leq\) 1; 1 \(\geq\) x \(\geq\) 2
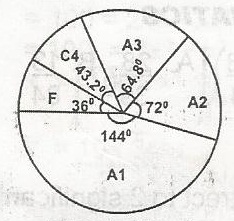
52.0
43.2
40.0
12.0
Correct answer is D
No explanation has been provided for this answer.
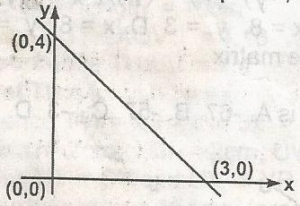
The equation of the line in the graph is
3y = 4x + 12
3y = 3x + 12
3y = -4x + 12
3y = -4x + 9
Correct answer is C
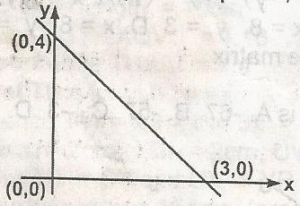
Gradient of line = \(\frac{\text{Change in y}}{\text{Change in x}} = \frac{y_2 - y_1}{x_2 - x_1}\)
y2 = 0, y1 = 4
x2 = 3 and x1 = 0
\(\frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 4}{3 - 0} = \frac{-4}{3}\)
Equation of straight line = y = mx + c
where m = gradient and c = y
intercept = 4
y = 4x + \(\frac{4}{3}\), multiple through by 3
3y = 4x + 12
2h
2\(\pi\)h
\(\pi\)h
\(\frac{\pi h}{2}\)
Correct answer is A
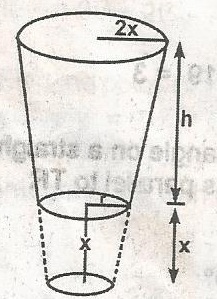
\(\frac{x}{r}\) = \(\frac{x + h}{2r}\)
2 x r = r (x + h)
Total height of cone = x + h
but x = h
total height = 2h
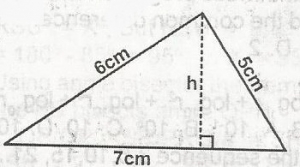
\(\frac{12}{7}\)cm
\(\frac{12}{7} \sqrt{6}\)cm
\(\frac{7}{12}\)cm
\(\frac{1}{2}\)cm
Correct answer is B
A\(\bigtriangleup\) = \(\sqrt{S(S - a) (S - b)(S - c)}\) (Hero's Formula)
S = \(\frac{a + b + c}{2}\) = \(\frac{5 + 6 + 7}{2}\)
\(\frac{18}{2} = 9\)
A\(\bigtriangleup\) \(\sqrt{9} \times 4 \times 3 \times 2\)
\(\sqrt{216} = 6 \sqrt{6}cm^3\)
A\(\bigtriangleup\) = \(\frac{1}{2} \times 6 \times h\)
6\(\sqrt{6} = \frac{1}{2} \times 7 \times h\)
h = \(\frac{12}{h} \sqrt{6}\)
JAMB Subjects
Aptitude Tests