The equation of the line in the graph is
...
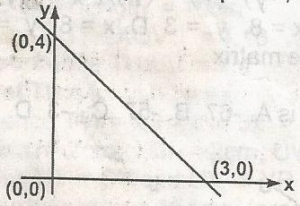
The equation of the line in the graph is
3y = 4x + 12
3y = 3x + 12
3y = -4x + 12
3y = -4x + 9
Correct answer is C
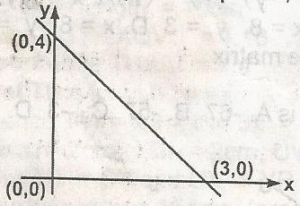
Gradient of line = \(\frac{\text{Change in y}}{\text{Change in x}} = \frac{y_2 - y_1}{x_2 - x_1}\)
y2 = 0, y1 = 4
x2 = 3 and x1 = 0
\(\frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 4}{3 - 0} = \frac{-4}{3}\)
Equation of straight line = y = mx + c
where m = gradient and c = y
intercept = 4
y = 4x + \(\frac{4}{3}\), multiple through by 3
3y = 4x + 12
Similar Questions
In the diagram, STUV is a straight line. < TSY = < UXY = 40o and < VUW = 110o. Calculate < TYW...
If f(x) = 2(x - 3)\(^2\) + 3(x - 3) + 4 and g(y) = \(\sqrt{5 + y}\), find g [f(3)] and f[g(4)]....
Find the values of k in the equation 6k2 = 5k + 6...
If (x - a) is a factor pf bx - ax + x2, find the other factor....
In the diagram above, TRQ is a straight line. Find p, if p = 1/3(a + b + c) ...