In the frustum of the cone, the top diagram is twice the ...
In the frustum of the cone, the top diagram is twice the bottom diameter. If the height of the frustum is h centimeters, find he height of the cone
2h
2\(\pi\)h
\(\pi\)h
\(\frac{\pi h}{2}\)
Correct answer is A
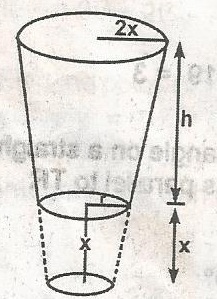
\(\frac{x}{r}\) = \(\frac{x + h}{2r}\)
2 x r = r (x + h)
Total height of cone = x + h
but x = h
total height = 2h
Similar Questions
If \(P344_{6} - 23P2_{6} = 2PP2_{6}\), find the value of the digit P. ...
In the diagram, ∠PMN = ∠PRQ and ∠PNM = ∠PQR. If /Pm/ = 3cm, /MQ/ = 7cm and /PN/ = 5c...
What is the median of the following scores: 22 35 41 63 74 82...
Find the product of 0.0409 and 0.0021 leaving your answer in the standard form ...
Solve the simultaneous equations 2x - 3y = -10, 10x - 6y = -5...