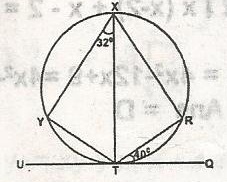
TQ is tangent to circle XYTR, < YXT = 32o, RTQ = 40o. find < YTR
108o
121o
140o
148o
Correct answer is A
< TWR = < QTR = 40o (alternate segment)
< TWR = < TXR = 40o(Angles in the same segments)
< YXR = 40o + 32o = 72o
< YXR + < YTR = 180o(Supplementary)
72o + < YTR = 180o
< YTR = 180o - 72o
= 108o
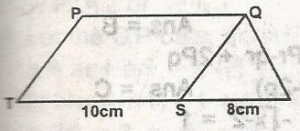
35cm2
65cm2
70cm2
140cm2
Correct answer is C
A\(\bigtriangleup\) = \(\frac{1}{2}\) x 8 x h = 20
= \(\frac{1}{2}\) x 8 x h = 4h
h = \(\frac{20}{4}\)
= 5cm
A\(\bigtriangleup\)(PQTS) = L x H
A\(\bigtriangleup\)PQRT = A\(\bigtriangleup\)QSR + A\(\bigtriangleup\)PQTS
20 + 50 = 70cm\(^2\)
ALTERNATIVE METHOD
A\(\bigtriangleup\)PQRT = \(\frac{1}{2}\) x 5 x 28
= 70cm\(^2\)
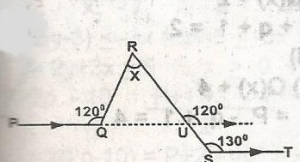
In diagram, PQ || ST and < PQR = 120o, < RST = 130o, find the angle marked x
50
65
70
80
Correct answer is C
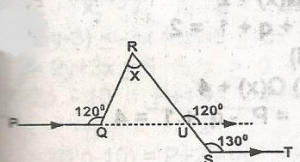
x + 60o + 50o = 180o
x = 110o = 180o
x = 180o - 110o
= 70o
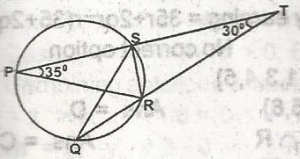
In the diagram, PR is a diameter of the circle PQRS. PST and QRT are straight lines. Find QRS
20o
25o
30o
35o
Correct answer is B
< PSR = \(\frac{1}{2}\)(180o) = 90o (angle substended by a semi-circle)
∴ < TSR = 90o
< SRT = 90o - 30o = 60o
< PRS = 90o - 35o = 55o
< PRQ = 180 - (60o + 55o) = 180 - 115o = 65o
< SQR = 35o(angles in the same segment)
< QSR + < SRQ + < SQR = 180o
< QSR + 120o + 35o = 180o
< QSR + 155 = 180o
< QSR = 180o - 155o
= 25o
x \(\leq\) 0, y \(\leq\) 0, 2y + 3x \(\leq\) 6
x \(\geq\) 0, y \(\geq\) 3, 3x + 2y \(\geq\) 6
x \(\geq\) 2, y \(\geq\) 0, 3x + 2y \(\leq\) 6
x \(\geq\) 0, y \(\geq\) 0, 3x + 2y \(\geq\) 6
Correct answer is A
m = \(\frac{y_2 - y_1}{x_2 - x_2} = \frac{3 - 0}{0 - 2} = \frac{-3}{2}\)
= \(\frac{y - y_1}{x- x_1}\)
m = \(\frac{y - 3}{x}\) \(\geq\) \(\frac{-3}{2}\)
2(y - 3) \(\geq\) - 3x = 2y - 6 \(\geq\) - 3x
= 2y + 3x \(\leq\) 6 ; x \(\leq\) 0, y \(\leq\) 0
JAMB Subjects
Aptitude Tests