Two angles of a pentagon are in the ratio 2:3. The others ar...
Two angles of a pentagon are in the ratio 2:3. The others are 60o each. Calculate the smaller of the two angles
A.
72o
B.
100o
C.
120o
D.
144o
Correct answer is D
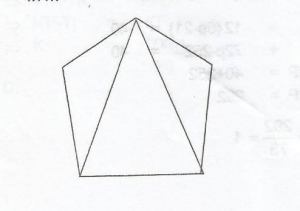
The diagram given simple illustrates that a pentagon contains three \(\Delta\)s.
Two angles which are in the ratio 2:3 will have actual values 2xo, 3xo respectively. Thus 2xo + 3xo + 3 x 60 = 3x sum of angles of \(\Delta\)a
i.e. 5xo + 180o = 3 x 180o
5xo + 180o = 540o
5xo = 540o - 180o
5xo = 360o
xo = \(\frac{360^o}{5}\)
= 72o
Hence, the smaller of the two angles is
2 x 72o = 144o
Similar Questions
Given that sin x = 3/5, 0 ≤ x ≤ 90, evaluate (tanx + 2cosx) ...
A worker's present salary is N24,000 per annum. His annual increment is 10% of his basic salary....
Factorize m\(^3\) - m\(^2\) + 2m - 2...
The straight line y = mx - 4 passes through the point(-4,16). Calculate the gradient of the line ...