The diagonals of a rhombus are 16 cm and 12 cm find the l...
The diagonals of a rhombus are 16 cm and 12 cm find the length of the side.
20cm
8cm
14cm
10cm
Correct answer is D
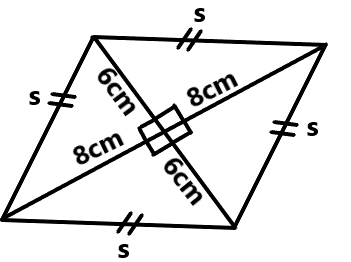
In a rhombus, the diagonals are perpendicular bisectors of each other, and they bisect the angles of the rhombus. This means that a rhombus is essentially made up of four congruent right-angled triangles.
We can use the Pythagorean theorem to find the length of one side of the rhombus (s)
\(s^2 = 8^2 + 6^2\)
\(s^2 = 64 + 36\)
\(s^2 = 100\)
s = \(\sqrt{100}\)
s =10 cm
So, the length of each side of the rhombus is 10 cm.
Similar Questions
If the pass mark was 4. What percentage of the pupils failed the test? ...
Evaluate \(log_{10}5 + log_{10}20\)...
A right circular cone has a base radius r cm and a vertical angle 2yo. The height of the cone is...
A sales boy gave a change of N68 instead of N72. Calculate his percentage error ...
Find the derivative of \(\frac {\sin\theta}{\cos\theta}\)...