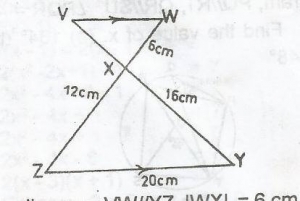
In the diagram, VW//YZ, |WX| = 6cm, |XY| = 16cm, |YZ| = 20cm and |ZX| = 12cm. Calculate |VX|
3cm
4cm
6cm
8cm
Correct answer is D
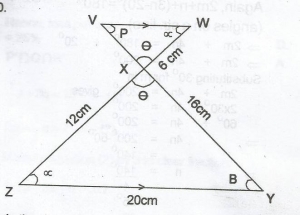
In the diagram, \(\frac{16}{12} = \frac{VX}{6}\) (similar \(\Delta\)s)
VX = \(\frac{16 \times 6}{12}\)
= 8cm
\(\frac{2}{5}\)
\(\frac{7}{60}\)
\(\frac{1}{30}\)
\(\frac{1}{60}\)
Correct answer is C
Hence the probability that only Kebba will hit the target
= P(K)xP(E')xP(O')
= \(\frac{2}{3} \times \frac{1}{4} \times \frac{1}{5}\)
= \(\frac{1}{30}\)
5.6
6.2
6.6
7.0
Correct answer is D
To calculate the mean of grouped data,
- First step to determine the midpoint (x) of each interval or class.
0 - 4 ►2
5 - 9 ► 7
10 - 14 ►12
These midpoints must then be multiplied by the frequencies of the corresponding classes:
2 X 2 = 4
1 X 7 = 7
2 X 12 = 24
Mean = ( 24 + 7 + 4) ÷ ( 2 + 1 + 2 )
: Mean = 7
62
63
64
65
Correct answer is C
Third quartile Q3 = \(\frac{3}{4}\)Nth
Alternatively:
Split the score into equal quarters
44, 47, 48, 49, 50, 51, 52, 53, 53, 54, 58, 59, 60, 61, 63, 65, 67, 70, 73, 75.
Third quartile Q3 = [63 + 65] / 2 = 64
32o
45o
60o
75o
Correct answer is A
In a school with students' population 810, the sectoral angle for a class of 72 students is
= \(\frac{72}{810}\) x 360º
= 32º
WAEC Subjects
Aptitude Tests