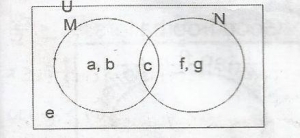
Examine M' \(\cap\) N from the venn diagram
{f, g}
{e}
{e, f, g}
{e, f, g}
Correct answer is A
From the venn diagram given,
M = (a, b, c), N = (c, f, g)
U = (a, b, c, d, e, f, g)
Thus M' \(\cap\) N = (e, f, g) \(\cap\) (c, f, g)
= (f, g)
70o
60o
55o
42o
Correct answer is B
Perimeter of a sector
= 2r + \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 21
64 = 2 x 21 + \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 21
64 = 42 + \(\frac{\theta}{360^o}\) x 44 x 3
64 - 42 = \(\frac{\theta}{360^o}\) x 11 x 3
22 = \(\frac{33\theta}{90}\)
\(\theta = \frac{22 \times 30}{11}\)
= 60o
96cm2
90cm2
81cm2
27cm2
Correct answer is C
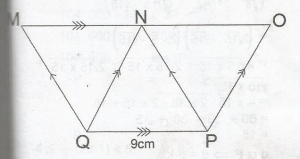
Area of \(\Delta\) QNP = \(\frac{1}{2} \times 9 \times 6 \) = 27cm2
Area of \(\Delta\) QMN = Area of \(\Delta\) QNP
= Area of \(\Delta\) PNO (triangles between the same parallels)
Hence, area of the trapezium
3 x area of \(\Delta\) QNP
= 3 x 27
= 81cm2
Express 1975 correct to 2 significant figures
20
1,900
1,980
2,000
Correct answer is D
No explanation has been provided for this answer.
\(\frac{2}{3}\)
2
3
6
Correct answer is C
Volume of sphere = Volume of cylinder
i.e. \(\frac{4}{3} \pi r^3 = \pi r^2 h\)
\(\frac{4}{3} \pi r^3 = \pi \times 3^2 \times 4\)
r3 = \(\frac{\pi \times 9 \times 4 \times 3}{4 \pi}\)
r = 3\(\sqrt{27}\)
= 3
WAEC Subjects
Aptitude Tests