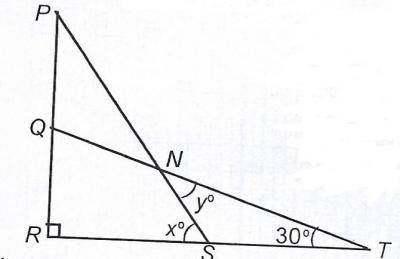
\(y = \frac{1}{2}x + 30\)
\(y = \frac{1}{2}x + 30\)
\(y = x + 30\)
\(y = x - 30\)
Correct answer is D
No explanation has been provided for this answer.
11.6 N
11.7 N
11.8 N
11.9 N
Correct answer is B
\(F = F \cos \theta i + F \sin \theta j\) (Resolving F into its components)
\(F_{1} = (10 N, 090°) = 10 \cos 90 i + 10 \sin 90 j\)
= \(10 j\)
\(F_{2} = (6 N, 180°) = 6 \cos 180 i + 6 \sin 180 j\)
= \(-6 i\)
\(R = - 6 i + 10 j\)
\(|R| = \sqrt{(-6)^{2} + (10)^{2}}\)
= \(\sqrt{136}\)
= 11.7 N
3.2 years
2.6 years
1.9 years
1.8 years
Correct answer is D
| \(x\) | 5 | 6 | 6 | 8 | 10 | Total |
| \(x - \bar{x}\) | -2 | -1 | -1 | 1 | 3 | |
| \((x - \bar{x})^{2}\) | 4 | 1 | 1 | 1 | 9 | 16 |
Mean (\(\bar{x}\)) = \(\frac{5 + 6 + 6 + 8 + 10}{5} \)
= \(\frac{35}{5} = 7\)
\(SD = \sqrt{\frac{\sum (x - \bar{x})^{2}}{n}}\)
= \(\sqrt{\frac{16}{5}} \)
= \(\sqrt{3.2}\)
\(\approxeq 1.8 years\)
\(\frac{3}{7}\)
\(\frac{21}{50}\)
\(\frac{7}{15}\)
\(\frac{49}{100}\)
Correct answer is C
\(P(\text{both bulbs are good}) = \frac{7}{10} \times \frac{6}{9}\)
= \(\frac{7}{15}\)
Express the force F = (8 N, 150°) in the form (a i + b j) where a and b are constants
\(4\sqrt{3} i - 4j\)
\(4 i - 4\sqrt{3} j\)
\(- 4 i + 4\sqrt{3} j\)
\(- 4\sqrt{3} i + 4j\)
Correct answer is D
\(F = F\cos \theta i + F \sin \theta j\)
\((8 N, 150°) = 8 \cos 150 i + 8 \sin 150 j\)
= \(- 8 \cos 30 i + 8 \sin 30 j\)
= \(-8(\frac{\sqrt{3}}{2}) i + 8(\frac{1}{2} j\)
= \(-4\sqrt{3} i + 4 j\)
WAEC Subjects
Aptitude Tests