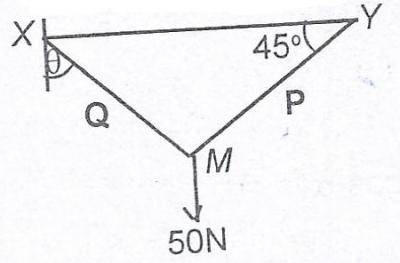
\frac{50 \cos \theta}{\sin (\theta + 45)°}
\frac{50 \cos \theta}{\cos (\theta + 45)°}
\frac{50 \sin \theta}{\cos (\theta + 45)°}
\frac{50 \sin \theta}{\sin (\theta + 45)°}
Correct answer is D
No explanation has been provided for this answer.
The distance between P(x, 7) and Q(6, 19) is 13 units. Find the values of x.
1 or -7
1 or 7
1 or 11
5 or -5
Correct answer is C
d = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}
13 = \sqrt{(x - 6)^{2} + (7 - 19)^{2}}
13^{2} = x^{2} - 12x + 36 + 144
169 = x^{2} - 12x + 180
x^{2} - 12x + 180 - 169 = 0 \implies x^{2} - 12x + 11 = 0
(x - 1)(x - 11) = 0 \implies x = \text{1 or 11}
If y = x^{2} - 6x + 11 is written in the form y = a(x - h)^{2} + k, find the value of (a + h + k).
-4
-3
0
6
Correct answer is D
y = x^{2} - 6x + 11
y = a(x - h)^{2} + k
a(x - h)^{2} + k = a(x^{2} - 2hx + h^{2}) + k
ax^{2} - 2ahx + ah^{2} + k = x^{2} - 6x + 11
Comparing, we have
a = 1
2ah = 6 \implies 2h = 6; h = 3
ah^{2} + k = 11 \implies (1 \times 3^{2}) + k = 11
9 + k = 11 \implies k = 2
\therefore a + h + k = 1 + 3 + 2 = 6
25
15
3\sqrt{7}
\sqrt{10}
Correct answer is A
Change in momentum = m (v - u)
= 5 \times (\begin{pmatrix} 4 \\ 7 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \end{pmatrix})
= 5 \times \begin{pmatrix} 3 \\ 4 \end{pmatrix}
= \begin{pmatrix} 15 \\ 20 \end{pmatrix}
|m(v - u)| = \sqrt{15^{2} + 20^{2}} = \sqrt{625} = 25
Find the value of the constant k for which a = 4 i - k j and b = 3 i + 8 j are perpendicular.
\frac{2}{3}
2
3
\frac{3}{2}
Correct answer is D
For perpendicular vectors, their dot product = 0.
(4i - kj). (3i + 8j) = 12 - 8k = 0
8k = 12 \implies k = \frac{3}{2}
WAEC Subjects
Aptitude Tests