103\(^o\)
123\(^o\)
133\(^o\)q
143\(^o\)
Correct answer is B
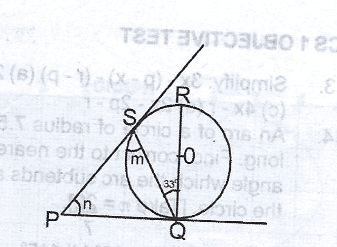
< SQP = 180 - (90 + 33) < on a ----
= 180 - (123)
= 57\(^o\)
Therefore, (m + n) = 123\(^o\)
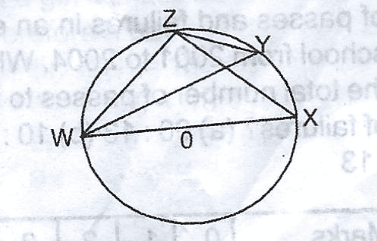
The diagram shows a circle O. If < ZYW = 33\(^o\) , find < ZWX
33\(^o\)
57\(^o\)
90\(^o\)
100\(^o\)
Correct answer is C
In ZY = 90\(^o\) < subtends In a semi O
ZWY = 180 - (90\(^o\) + 33)
= 57
ZWX = 57 + 33 = 90\(^o\)
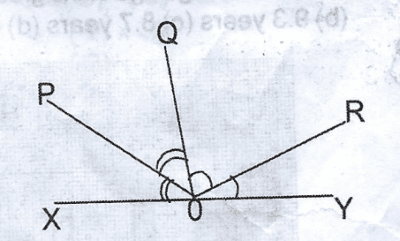
In the diagram, XY is a straight line.
60\(^o\)
90\(^o\)
100\(^o\)
120\(^o\)
Correct answer is B
<POX = <POQ; <ROY = QOR
2 <POQ + 2 <ROY = 180
2(<POQ = <ROY) = 180
<POQ + <ROY = 90
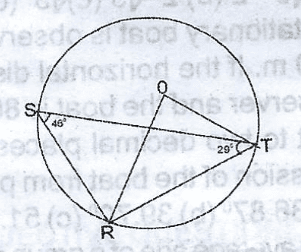
The diagram shows a circle centre O. if <STR = 29 and <RST = 45, calculate the value of <STO
12\(^o\)
15\(^o\)
29\(^o\)
34\(^o\)
Correct answer is A
SRT = 180 - (46 + 29) sum of < s in a
= 180 - 75
= 105
SOT = 2 x 46 < at the centre is twice all the circle = 92
RTO = 180 - (96 + 43)
= 41
STO = 41 - 29
= 12\(^o\)

1
2
3
4
Correct answer is C
(n \(\oplus\) 4) \(\oplus\) 3 = 0 (mod 5)
(3 \(\oplus\) 4) \(\oplus\) 3
12 \(\oplus\) 3 = 15 (mod 5)
(5 x 3 + 0) = 0 (mod 5)
WAEC Subjects
Aptitude Tests