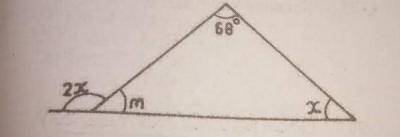
Find the value of m in the diagram
72\(^o\)
68\(^o\)
44\(^o\)
34\(^o\)
Correct answer is C
2x + m = 180
x + m = 112
x = 122 - m
2(112 - m) + m = 180
224 - 2m + m = 180
224 - m = 180
224 - 180 = m
m = 44\(^o\)
The diagonal of a square is 60 cm. Calculate its peremeter
20\(\sqrt{2}\)
40\(\sqrt{2}\)
90\(\sqrt{2}\)
120\(\sqrt{2}\)
Correct answer is D
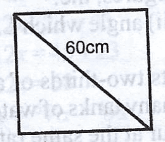
\(60^2 + x^2 + x^2\)
\(360^2 = 2x^2\)
\(x^2\) = 1800
x = \(\sqrt{1800}\)
x = 42.4264
x = 42.4264
perimeter = 4x
= 4 x 42.4264
= 169.7056
= 120\(\sqrt{2}\)
= 120\(\sqrt{2}\)
36.87\(^o\)
39.70\(^o\)
51.34\(^o\)
53.13\(^o\)
Correct answer is C
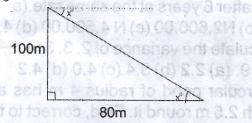
Tan \(x^o = \frac{100m}{80}\)
Tan \(x^o = Tan^{-1} 1.25\)
x = 51.34\(^o\)
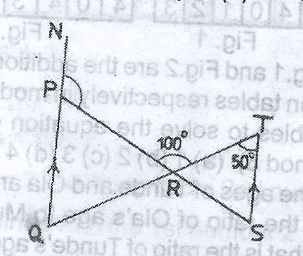
In the diagram, NQ//TS, <RTS = 50\(^o\) and <PRT = 100\(^o\). Find the value of <NPR
110\(^o\)
130\(^o\)
140\(^o\)
150\(^o\)
Correct answer is B
< TSR = 180 - (80 + 50)
= 180 - (130)
= 50\(^o\)
< QPR = < TSR corresponding < s
< NPR + QPR = < NPR
180\(^o\) - < QPR = < NPR
180\(^o\) - 50 = < NPR
< NPR = 130\(^o\)
\(\frac{2}{9}\)
\(\frac{4}{9}\)
\(\frac{5}{9}\)
\(\frac{7}{9}\)
Correct answer is B
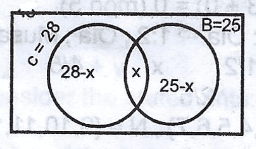
28 - x + x + 25 - x = 45
53 - x = 45
x = 53 - 45
x = 8
chemistry only = 28 - 8
= 20
Probability = \(\frac{20}{45}\)
= \(\frac{4}{9}\)
WAEC Subjects
Aptitude Tests