| Marks | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 7 | 4 | 18 | 12 | 8 | 11 |
The table gives the distribution of marks obtained by a number of pupils in a class test. Using this information, Find the median of the distribution
4
3
1
2
Correct answer is B
Median is n2=62
= 3
Median = 3
Factorise (4a + 3) 2 - (3a - 2)2
(a + 1)(a + 5)
(a - 5)(7a - 1)
(a + 5)(7a + 1)
a(7a + 1)
Correct answer is C
[(4a + 3) 2 - (3a - 2)2 = a2 - b2 = (a + b) (a - b)
= [(4a + 3) + (3a - 2)] [(4a + 3) - (3a - 2)]
= [4a + 3 + 3a - 2] [4a + 3 - 3a + 2]
= (7a + 1)(a + 5)
(a + 5) (7a + 1)
How much did he spend on food items?
N9,700.00
N6,700.00
N2,000.00
N4,000.00
N2,300.00
Correct answer is E
Degree for food items = 360° - (120° + 80° + 43° + 30° + 18°)
= 360° - 291°
= 69°
∴∴ Amount spent on food items = 69360×12,000.00
= N2300.00
24o
42o
48o
66o
Correct answer is A
RSP = 90 < substance in semi a circle
RPS = 180 - (90 + 24)
= 180 - (114)
= 66
TPS = 180 - 66
= 114
RST = 24
< STR = 180 - (114 + 24)
= 180 - 138
= 42o
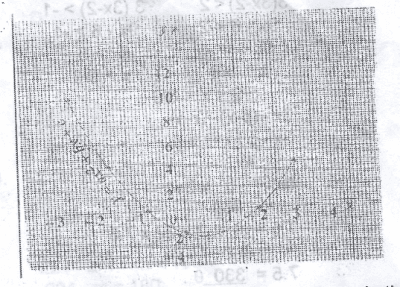
The graph of y = ax2+bx+c is shown oon the diagram. Find the minimum value of y
-2, 0
-2, 1
-2, 3
-2, 5
Correct answer is B
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests