206.
A.
6.6 cm
B.
8.8 cm
C.
4.4 cm
D.
2.2 cm
Correct answer is C
Length = θ360 x 2πr
= 72360×2227×0.53.5
= 4.4
207.
If logx 2 = 0.3, evaluate logx 8.
A.
2.4
B.
1.2
C.
0.9
D.
0.6
Correct answer is C
logx2 = 0.3
logx8 = logx23 = 3 logx2
= 3 x 0.3
= 0.9
208.
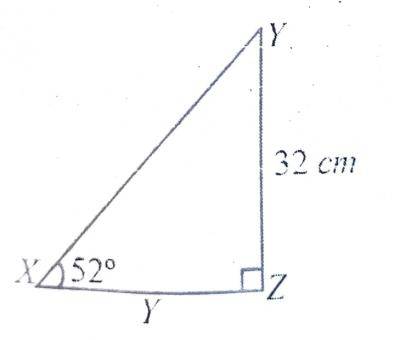

In XYZ, |YZ| = 32cm, < YXZ 53o and XZY = 90o. Find, correct to the nearest centimetre, |XZ|
A.
31 cm
B.
25 cm
C.
20 cm
D.
13 cm
Correct answer is B
Tan 52o = 32|XZ|
|XZ| = 32Tan52o
= 25cm
209.
If 2a = √64 and ba = 3, evaluate a2+b2
A.
250
B.
160
C.
90
D.
48
Correct answer is C
2a = √64
2a = 8
2a = 23
a = 3
b = 3a
b = 3 x 3 = 9
a2 + b2 = 32 + 92
= 9 + 81 = 90
210.
A.
7.5 cm
B.
4.5 cm
C.
4.0 cm
D.
2.0 cm
Correct answer is C
165 = 2 x 227 x 72 x h + 2 x 227 x 72 x 72
165 = 22h + 77
22h22=8822
height = 4cm
WAEC Subjects
Aptitude Tests