176.
Solve, correct to three significant figures, (0.3)x = (0,5)8
A.
4.61
B.
4.606
C.
0.461
D.
0.0130
Correct answer is A
(0,3)x = (0.5)8
xlog 0,3 = 9 log 0.5
x = 8log0.5log0.3
= 4.606
178.
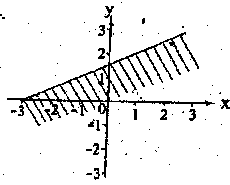

Which of these inequalities is represented by the shaded portion of the graph?
A.
2y + x - 3 < 0
B.
2y - x - 3 < 0
C.
2y - x + 3 < 0
D.
2y + x +3 < 0
Correct answer is B
(0, 1.5), (-3, 0)
m = 0−1.5−3,0 = 0.5
0.5 = y−1.5−3.0 = 0.5
y = 0.5x + 1.5
2y = x + 3
2y - x - 3 < 0
179.
Find the constant term in the binomial expansion of (2x2 + 1x2)4
A.
10
B.
12
C.
24
D.
42
Correct answer is B
6(2x2)2 (1x2)2
= 6 x 2
= 12
180.
A.
12m
B.
16m
C.
64m
D.
96m
Correct answer is B
V = 3t2 - 6t
dsdt=3t2−6t
s = ∫3t2−6t
s = 3t33−6t22+k
s = t3 - 3t2 + k
s = 0, t = 0
s = t3 - 3t2
s = 43 - 3t2
s = 43 - 3(4)2
= 64 - 48 = 16m
WAEC Subjects
Aptitude Tests