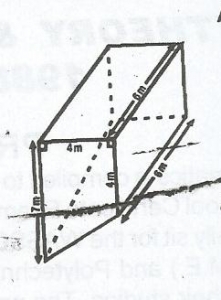
66m3
84m3
132m3
168m3
264m3
Correct answer is C
Area of trapezium = 1/2(a+b)h
= 1/2(4 + 7)x4 = 22m2
volume = 22 x 6 = 132m3
What is the probability of having an odd number in a single toss of a fair die?
1/6
1/3
1/2
2/3
5/6
Correct answer is C
n(S) = 6(odd) = {1, 3, 5}
n(odd) = 3
pr(odd) = \(\frac{n(odd)}{n(S)}\) 3/6 =1/2
A sales girl gave a change of N1.15 to a customer instead of N1.25. Calculate her percentage error
10%
7%
8.0%
2.4%
10%
Correct answer is C
Error = 1.25 - 1.15 = 0.10
0.10/1.25
* 100 = 8.0%
Find the quadratic equation whose roots are x = -2 or x = 7
x2 + 2x - 7 = 0
x2 - 2x + 7 = 0
x2 + 5 +14 = 0
x2 - 5x - 14 = 0
x2 + 5x - 14 = 0
Correct answer is D
x + 2 and x - 7 are factors
(x+2)(x+7) = 0
x(x-7) + 2(x-7) = 0
x2 - 7x + 2x - 14 = 0
x2 - 5x - 14 = 0
x = 1
x = -1
y = 1
y = -1
x + y = 1
Correct answer is C
The linear equation will be the difference between the equation.
y=x2 + 4x - 6 and x2 + 4x - 7 = 0
y=x2 + 4x - 6, ( 0 = x2 + 4x - 7)
y = -(-1) y = 1
WAEC Subjects
Aptitude Tests